КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Идеальная изображающая система преобразует расходящийся сферический световой пучок из каждой точки предмета в сферический пучок, сходящийся в соответствующую точку изображения. Оптические длины путей разных лучей при этом одинаковы. Реальные изображающие системы, состоящие из линз и зеркал, не являются идеальными вследствие двух основных причин: геометрических отклонений хода лучей от идеального - геометрических аберраций и дифракционных явлений, возникающих на краях апертур линз или зеркал. Дифракционные явления носят фундаментальный характер и определяют предельные возможности оптических систем. Часто дифракционные явления пренебрежимо малы по сравнению с геометрическими аберрациями, и в таких случаях качество изображающей системы определяется ее геометрическими аберрациями. Формирование изображения в оптической системе можно рассматривать так: гомоцентрический пучок лучей из точки с координатами
Рис.2.3. Схема формирования изображения точки Волновыми фронтами являются сферы с центром в точке Это явление и есть аберрация. Для вычисления аберраций вводится два понятия - волновая (или продольная) и геометрическая (или поперечная) аберрации. Вектор
Рис. 2.4. Геометрические и волновые аберрации Вектор поперечной аберрации
Для центрированных оптических систем
При этом геометрические аберрации
Как видно, Коэффициенты B, C, D, E и F соответствуют различным типам аберраций, дающим различные искажения изображения: 1. 2. При наличии астигматизма у оптической системы, резкие изображение по осям x и y наблюдаются при различных значениях z. 3. 4. 5.
Рис.2.5. Измерение геометрических аберраций Существует несколько методов измерения геометрических и волновых аберраций. Наиболее простым и наглядным является так называемый метод внефокальных наблюдений. Применимость его ограничена в основном измерением сферической аберрации, что и будет предметом более подробного исследования в настоящей лабораторной работе. Суть метода заключается в следующем: выбираются две плоскости наблюдения по разные стороны от изображения точки (см. рис 2.5). Лучи, прошедшие через линзу на разных расстояниях от оптической оси, имеют разные смещения изображения точки от так называемого параксиального изображения, соответствующего центральной части линзы. На рис.2.5 показаны две зоны, из которых одна считается параксиальной и строит параксиальное изображение точки на расстоянии R от линзы. Номер этой зоны n =0 наименьший. Для другой показанной зоны изображение смещено на D f относительно параксиального изображения и лучи, идущие из нее, имеют поперечные отклонения D от параксиального изображения. Для того чтобы вычислить это смещение D f, а также отклонение лучей D, проводят измерения соответствующих диаметров
Таким же образом можно измерить диаметры в двух плоскостях наблюдения
|

 (рис.2.3) проходит через входной зрачок оптической системы к выходному зрачку. Если изображающая система идеальна, то пучок, проходящий через выходной зрачок, является гомоцентрическим, сходящимся в точку плоскости изображения с координатами, равными координатам сопряженной точки изображения. При приведении масштаба предмета к масштабу изображения координата сопряженной точки численно равна координате
(рис.2.3) проходит через входной зрачок оптической системы к выходному зрачку. Если изображающая система идеальна, то пучок, проходящий через выходной зрачок, является гомоцентрическим, сходящимся в точку плоскости изображения с координатами, равными координатам сопряженной точки изображения. При приведении масштаба предмета к масштабу изображения координата сопряженной точки численно равна координате 
 выходного зрачка, приходит в точку с координатами
выходного зрачка, приходит в точку с координатами 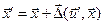 вместо точки
вместо точки  , характеризующий поперечную аберрацию в точке
, характеризующий поперечную аберрацию в точке  . Для введения волновой аберрации
. Для введения волновой аберрации  наряду с опорной сферой Гаусса рассматривают реальный волновой фронт s, проходящий также через центр выходного зрачка (см. рис. 2.4). Оптическая длина пути
наряду с опорной сферой Гаусса рассматривают реальный волновой фронт s, проходящий также через центр выходного зрачка (см. рис. 2.4). Оптическая длина пути 
 пропорционален двумерному градиенту от функции волновой аберрации
пропорционален двумерному градиенту от функции волновой аберрации  ,
,  . (2.10)
. (2.10) . При разложении в ряд
. При разложении в ряд  (2.11)
(2.11)

 - сферическая аберрация. При наличии сферической аберрации для лучей, проходящих на разных расстояниях от оптической оси, фокусные расстояния различны (рис.2.5).
- сферическая аберрация. При наличии сферической аберрации для лучей, проходящих на разных расстояниях от оптической оси, фокусные расстояния различны (рис.2.5). - астигматизм.
- астигматизм. - кривизна поля (резкое изображение получается на кривой поверхности).
- кривизна поля (резкое изображение получается на кривой поверхности).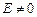 - дисторсия (изображение резкое, но присутствуют геометрические искажения).
- дисторсия (изображение резкое, но присутствуют геометрические искажения).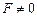 - кома (изображение точки содержит “хвост”).
- кома (изображение точки содержит “хвост”).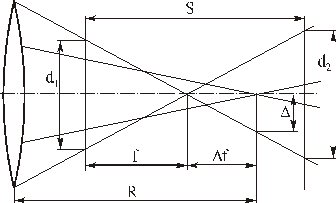
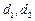 в двух плоскостях наблюдения, отстоящих друг от друга на расстояние s, и далее из подобия треугольников вычисляется расстояние от изображения точки от плоскости наблюдения:
в двух плоскостях наблюдения, отстоящих друг от друга на расстояние s, и далее из подобия треугольников вычисляется расстояние от изображения точки от плоскости наблюдения: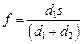 . (2.12)
. (2.12) (где n ‑ номер зоны) для всех остальных зон и вычислить
(где n ‑ номер зоны) для всех остальных зон и вычислить  для всех зон. Теперь для того, чтобы найти соответствующие
для всех зон. Теперь для того, чтобы найти соответствующие  для всех зон (кроме нулевой), необходимо воспользоваться соотношениями
для всех зон (кроме нулевой), необходимо воспользоваться соотношениями ,
,  . (2.13)
. (2.13)


