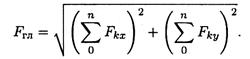Практическое занятие №2. Плоская система произвольно расположенных сил

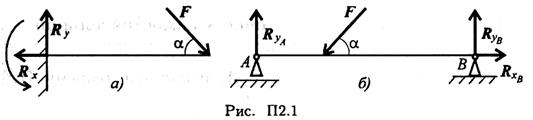
Знать теорему Пуансо о приведении силы к точке.

Уметь приводить произвольную плоскую систему сил к точ­ке, определяя величины главного вектора и главного момента сис­темы.

Знать три формы уравнений равновесия и уметь ими пользо­ваться при определении реакций в опорах балочных систем.

Основные формулы и предпосылки расчета

Виды опор балок и их реакции (рис. П2.1)

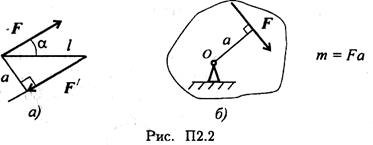
Моменты пары сил и силы относительно точки (рис. П2.2)

Главный вектор

Главный момент

Условия равновесия

Проверка:

Проверка:

Упражнения при подготовке к самостоятельной работе

4. Перенести силу F в точку А, используя теорему Пуансо (рис. П2.3).

F = 20кН; АВ = 6м; ВС = 2м.

 

2. Привести систему сил к точке В, определить главный вектор и главный момент системы сил (рис. П2.4). АВ = 2м; ВС = 1,5м; CD = 1м. F₁ = 18кН; F₂ = 10кН; F₃ = 30кН; т = 36кН-м.

 

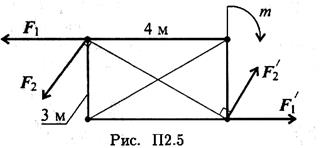
3. Система сил находится в равновесии. Определить величину момента пары т (рис. П2.5).

F₁ = F₁’ = 10 кН; F₂ = F₂’ = 20кН.

 

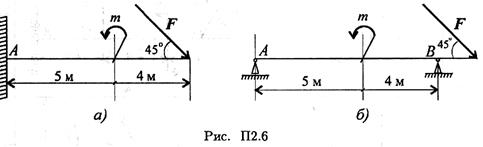
4. Нанести реакции в опорах балок 1 и 2 (рис. П2.6).

 

 

5. Определить величину реакции в опоре А. Приложена распре­деленная нагрузка интенсивностью q = 5кН/м (рис. П2.7).

 

6. Записать систему уравнений равновесия для определения ре­акций в опоре защемленной балки.

7. Записать систему уравнений равновесия для определения ре­акций в опорах двухопорной балки, закрепленной на двух шарнирах.