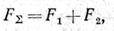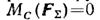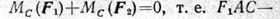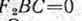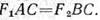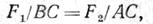Решение. 1. Находим модуль равнодействующей
1. Находим модуль равнодействующей. Как известно,
Но если ось х расположить перпендикулярно силам, а ось у — параллельно (рис. 1.47, а), направив ее положительный отсчет вниз, то проекции каждой из сил на ось х равны нулю и, значит,
а проекции сил на ось у равны их модулям с соответствующими знаками: F1y = F1 = 6 Н; F2y= F2 = 8 H; F3y = F3 = 10 H; F4y = F4 = 15 Н и F5y = F5 = 3H. Таким образом, модуль равнодействующей системы параллельных сил
Вектор равнодействующей FΣ направлен параллельно составляющим силам в сторону положительного отсчета оси у, если XFky > 0, и в сторону отрицательного отсчета, если ΣFky < 0.
В данном случае FΣ = ΣFк = 6 — 8 + 10 + 15 — 3 = 20 Н, т. е. равнодействующая равна 20 Н и направлена вниз. 2. Изобразим эту равнодействующую условно штриховой линией на некотором расстоянии х от начала координат (рис. а) и запишем моменты всех сил относительно точки Ах'
И, согласно теореме Вариньона, получим — FΣx = F2 * A1A2 – F3 * A1A3 – F4 * A1A4 + F5 * A1A5 Отсюда после подстановки известных числовых значений сил и плеч —20 x = 8 – 0,2 — 10 – 0,4 — 15 – 0,6 + 3 – 0,8, получим
Следовательно, FΣ = 20 Н, а ее линия действия, параллельная составляющим силам, проходит от точки A1 на расстоянии l = 0,45 м (рис. 1.47,6).
Даны приложенные к телу параллельные силы F1 и F2, направленные в одну сторону. Согласно равенству FΣ = ΣFk ясно, что в данном случае
а вектор равнодействующей FΣ, приложенный в некоторой точке С, направлен параллельно силам в ту же сторону. Возьмем сумму моментов сил относительно точки С (точки, через которую проходит линия действия равнодействующей). Тогда
и, следовательно,
или
отсюда получаем известную из физики пропорциональную зависимость:
т. е. расстояния от линии действия двух параллельных сил до линии действия равнодействующей обратно пропорциональны силам.
Легко доказать (проделайте это самостоятельно), что такую же зависимость получим и при определении равнодействующей двух параллельных сил, направленных в противоположные стороны, хотя в этом случае модуль равнодействующей FΣ = F1 — F2. Направлена она в сторону большей по модулю силы, и линия ее действия расположена не между слагаемыми силами, а за большей из них (рис. б).
|

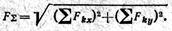
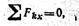
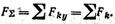
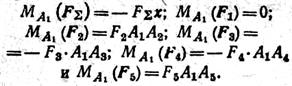
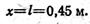
 Известные из физики зависимости, возникающие при сложении двух параллельных сил, можно получить из теоремы Вариньона.
Известные из физики зависимости, возникающие при сложении двух параллельных сил, можно получить из теоремы Вариньона.