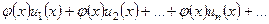Равномерная сходимость
Рассмотрим функциональный ряд, сходящийся в некоторой области. Обозначим сумму ряда через
Говорят, что ряд сходится к функции Определение. Сходящийся функциональный ряд (1) называется равномерно сходящимся в некоторой области, если каждому сколь угодно малому числу Если ряд
с одной и той же точностью во всех точках рассматриваемого интервала; эта точность характеризуется неравенством Теорема. Сумма равномерно сходящегося в некоторой области ряда, составленного из непрерывных функций, есть функция, непрерывная в этой области. Признак Вейерштрасса (достаточный признак равномерной сходимости). Пусть а) в некоторой области б) числовой ряд то функциональный ряд Пример. Функциональный ряд
сходится равномерно для всех действительных
и обобщенный гармонический ряд Как мы знаем, сумму конечного числа функций можно почленно дифференцировать и интегрировать. Эти свойства не всегда выполняются, если число слагаемых бесконечно, т.е. для рядов. Однако эти свойства сохраняются для равномерно сходящихся на сегменте функциональных рядов. Теорема 1. Если члены равномерно сходящегося на сегменте Это значит, что если
Теорема 2. Пусть ряд Итак, применимость действий анализа к бесконечному функциональному ряду обеспечивается свойством равномерной сходимости ряда. Применимость арифметических действий к бесконечному ряду обеспечивается свойством абсолютной сходимости ряда Теорема 3. Если равномерно сходящийся на сегменте
будет равномерно сходящимся на сегменте
|

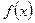 , тогда для всех
, тогда для всех 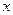 из области сходимости имеем
из области сходимости имеем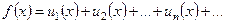 (1)
(1)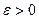 соответствует такое целое положительное число
соответствует такое целое положительное число 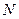 , что
, что 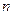 -ый остаток
-ый остаток  при
при 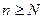 остается по абсолютной величине меньше
остается по абсолютной величине меньше 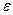 , каково бы ни было
, каково бы ни было 
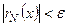 , справедливым при любом рассматриваемом
, справедливым при любом рассматриваемом 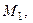
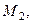 …,
…,  … – положительные числа. Если
… – положительные числа. Если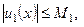
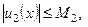 …,
…, 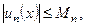 …;
…;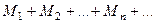 сходится,
сходится,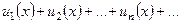 в этой области сходится равномерно (и абсолютно).
в этой области сходится равномерно (и абсолютно).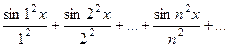
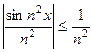 ,
,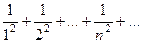 с показателем
с показателем 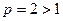 сходится. ●
сходится. ●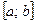 функционального ряда
функционального ряда 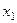 и
и 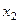 любые две точки сегмента
любые две точки сегмента 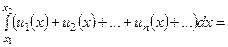
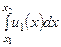 +
+  + …
+ … 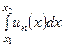 + …
+ …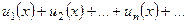 умножить на ограниченную функцию
умножить на ограниченную функцию 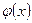 , то полученный ряд
, то полученный ряд