Остаток ряда и его оценка
Рассмотрим сходящийся ряд
Его сумма Определение. Разность между суммой ряда Остаток ряда обозначается
Абсолютная погрешность при замене суммы ряда
Таким образом, если требуется найти суму ряда с точностью до Теорема. Если знакочередующийся ряд сходится по признаку Лейбница, то его
Пример. Найти с точностью до 10-3 сумму ряда Ряд сходится, т. к. удовлетворяет всем условиям признака Лейбница. По правилу оценки погрешности вычисления надо взять столько членов, чтобы выполнялось неравенство
Тогда остаток ряда, начинающийся с этого члена, будет также меньше 10-3. Следовательно, решаем неравенство:
Это неравенство удовлетворяется уже при Следовательно, начиная с члена
Глава 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ Основные понятия Определение. Выражение
называется функциональным рядом относительно переменной х. Придавая
Этот ряд может сходиться или расходиться. Если он сходится, то точка Определение. Совокупность всех точек сходимости функционального ряда называется областью его сходимости. Частичная сумма функционального ряда, т.е. сумма первых его
является функцией переменной Каждому значению В этом случае пишут
Если функциональный ряд сходится и имеет сумму
называется остатком функционального ряда. В простейших случаях для определения области сходимости ряда (1) достаточно применить к этому ряду известные признаки сходимости положительных рядов, считая Пример 1. Найти область сходимости ряда
Решение. Если Если Итак, область сходимости ряда определяется неравенством
|
(1)
, где 
.
и его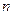 
-ой частичной суммой 
называется 
:
.
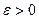, то надо взять сумму такого числа 
.
.
.
.
.
: 
.
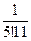, можно отбросить все члены ряда и вычислить только первыепять членов ряда.
.●
,(1)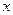
какое-либо значение 
из области определения функций 
, получим числовой ряд
(2)
(3)
соответствует определенное значение величины 
. Эту величину обозначают через 
и называют суммой функционального ряда. Итак, сумма 
функционального ряда есть некоторая функция переменной 
.
, то 
; так как 
, то ряд расходится. Если 
, то также получаем расходящийся ряд 
.
, то члены заданного ряда меньше членов геометрического ряда 
со знаменателем 
, т.е. ряд сходится.
или 
.●
