Ряды и коэффициенты Фурье
Многие процессы, происходящие в природе и технике, обладают свойством повторяться через определенные промежутки времени. Такие процессы называются периодическими. Примерами периодических процессов могут служить движение поршня в двигателях, распространение электромагнитных колебаний и т.п. Периодические процессы описываются периодическими функциями. Простейшими периодическими функциями являются тригонометрические функции Тригонометрические ряды были введены Бернулли (швейцарец, математик и механик, один из основоположников гидродинамики) в 1753 г. в связи с изучением колебаний струны. Формулы, выражающие коэффициенты ряда через данную функцию, были даны французским математиком Клеро в 1757 г., но не привлекли к себе внимания. Эйлер вновь получил эти формулы в 1777 г. (в работе, опубликованной после смерти Эйлера в 1793 г.). Строгий их вывод был намечен Фурье в 1823 г. Фурье систематически пользовался тригонометрическими рядами при изучении задач теплопроводности. Итак, простейший периодический процесс – гармоническое колебание – описывается периодическими функциями Рассмотрим функциональный ряд вида
Такой ряд называется тригонометрическим рядом. Так как члены тригонометрического ряда (1) имеют общий период Если периодическая функция
Коэффициенты ряда, определенные по этим формулам, называются коэффициентами Эйлера-Фурье. Определение. Тригонометрический ряд
коэффициенты которого определяются по формулам Эйлера-Фурье, называется рядом Фурье, соответствующим функции Теорема Дирихле. Если функция
|

 и
и  . В электромеханике и электротехнике часто встречаются периодические несинусоидальные функции. Они могут описывать как механические колебания, так и электрические величины, например, пилообразные или в форме трапеции напряжения и токи. Для удобства работы эти функции можно разложить в тригонометрические ряды, т.е. представить их в виде суммы синусов, косинусов и свободного члена.
. В электромеханике и электротехнике часто встречаются периодические несинусоидальные функции. Они могут описывать как механические колебания, так и электрические величины, например, пилообразные или в форме трапеции напряжения и токи. Для удобства работы эти функции можно разложить в тригонометрические ряды, т.е. представить их в виде суммы синусов, косинусов и свободного члена.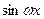 и
и  . Более сложные периодические процессы описываются функциями, составленными либо из конечного, либо из бесконечного числа слагаемых вида
. Более сложные периодические процессы описываются функциями, составленными либо из конечного, либо из бесконечного числа слагаемых вида 
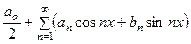 (1)
(1) , то и сумма ряда, если он сходится, будет также периодической функцией с периодом
, то и сумма ряда, если он сходится, будет также периодической функцией с периодом 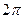 .
. является суммой равномерно сходящегося на сегменте
является суммой равномерно сходящегося на сегменте  тригонометрического ряда (1), то коэффициенты этого ряда определяются по формулам:
тригонометрического ряда (1), то коэффициенты этого ряда определяются по формулам: ,
,  ,
,  .
. ,
,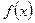 задана на сегменте
задана на сегменте 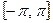 и является на нем кусочно непрерывной, кусочно монотонной и ограниченной, то ее тригонометрический ряд Фурье сходится во всех точках сегмента
и является на нем кусочно непрерывной, кусочно монотонной и ограниченной, то ее тригонометрический ряд Фурье сходится во всех точках сегмента  – сумма этого ряда, то во всех точках непрерывности этой функции
– сумма этого ряда, то во всех точках непрерывности этой функции


