Ряд, составленный из абсолютных величин его членов
Сходится, то данный знакопеременный ряд также сходится. Пример 1. Исследуем на сходимость знакопеременный ряд
Решение. Рассмотрим ряд, составленный из абсолютных величин данного ряда
Этот ряд сходится, как обобщенный гармонический ряд с показателем Пример 2. Рассмотрим знакочередующийся ряд
который сходится по признаку Лейбница. Но ряд, составленный из абсолютных величин данного ряда
является гармоническим и, следовательно, расходится.● Определение 1. Знакопеременный ряд Определение 2. Знакопеременный ряд Ряд, рассмотренный в примере 1, является абсолютно сходящимся, в примере 2 – условно сходящимся. Теорема 1. Сумма абсолютно сходящегося ряда не меняется от любой перестановки его членов. Теорема 2. Два абсолютно сходящихся ряда можно перемножать по правилу умножения конечных сумм. Полученный в результате умножения ряд абсолютно сходится и его сумма равна произведению сумм исходных рядов.
|




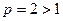 . Следовательно, на основании достаточного признака сходится и данный ряд. ●
. Следовательно, на основании достаточного признака сходится и данный ряд. ●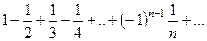 ,
,
 называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.


