Если ряд (2) сходится, то ряд (1) также сходится,
2) если ряд (1) расходится, то ряд (2) также расходится. Замечание. Признаки сравнения применимы и в том случае, когда условие Пример 1. Исследовать на сходимость ряд Решение. Оценим общий член данного ряда: Пример 2. Исследовать на сходимость ряд Решение. Рассмотрим вспомогательный ряд
который расходится (см. пример 3, §4). Так как
то по теореме 1(п.2) данный ряд также расходится. ● Теорема 2 (второй признак сравнения рядов). Пусть даны два знакоположительных ряда Смысл этого признака состоит в том, что если общий член ряда (1) и общий член ряда (2) являются бесконечномалыми одного и того же порядка (при При исследовании сходимости рядов с помощью признаков сравнения необходимо иметь для сравнения ряды, относительно которых известно, сходятся они или расходятся. В качестве таких рядов часто используют геометрический ряд, а также
который сходится при При
Пример 1. Исследуем сходимость ряда Решение. Рассмотрим вспомогательный ряд Вычисляем Пример 2. Исследуем сходимость ряда Решение. Рассмотрим вспомогательный ряд Вычисляем
|

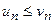 выполняется не при всех n, а лишь начиная с некоторого n = N.
выполняется не при всех n, а лишь начиная с некоторого n = N. .
. . Ряд с общим членом
. Ряд с общим членом  сходится (геометрический ряд). По теореме 1(п.1) данный ряд также сходится.●
сходится (геометрический ряд). По теореме 1(п.1) данный ряд также сходится.● .
. ,
, ,
, (1) и
(1) и  (2). Если существует конечный, отличный от нуля, предел отношения общих членов этих рядов:
(2). Если существует конечный, отличный от нуля, предел отношения общих членов этих рядов:  , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.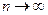 ), то сходимость одного из этих рядов влечет сходимость другого (а значит, и, наоборот, расходимость одного влечет расходимость другого).
), то сходимость одного из этих рядов влечет сходимость другого (а значит, и, наоборот, расходимость одного влечет расходимость другого).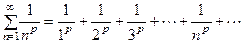 – обобщенный гармонический ряд,
– обобщенный гармонический ряд, и расходится при
и расходится при  . Это будет доказано ниже.
. Это будет доказано ниже. получается
получается – гармонический ряд.
– гармонический ряд. .
.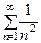 , который сходится.
, который сходится. . Значит, по теореме 2 данный ряд сходится. ●
. Значит, по теореме 2 данный ряд сходится. ●
 , который расходится.
, который расходится. . Значит, по теореме 2 данный ряд расходится. ●
. Значит, по теореме 2 данный ряд расходится. ●


