Лабораторна робота №4
Синтез дешифраторів та шифраторів Мета роботи:навчитися проектувати комбінаційні схеми і дослідити роботу дешифратора, шифратора. Програмне забезпечення: Circuit Maker 5. 1. Теоретичні відомості Дешифратор – комбінаційний пристрій, який перетворює комбінацію вхідних змінних в активний сигнал “лог. 1” або “лог. 0” тільки на одному із виходів. Дешифратори і шифратори належать до перетворювачів кодів. Максимальна кількість виходів дешифратора дорівнює Якщо частина вхідних наборів не використовується, то дешифратор називається неповним і у нього Якщо вхідні змінні представити як двійкову систему запису чисел, то логічна одиниця формується на тому виході, номер якого відповідає десятковому запису числа. Наприклад: Дешифратори широко використовуються в якості перетворювачів двійкового коду в десятковий. В ЕОМ з допомогою дешифраторів здійснюється вибірка необхідних комірок запам’ятовуючих пристроїв, розшифровка кодів операцій з видачею відповідних керуючих сигналів. В умовних позначеннях дешифраторів і шифраторів використовуються букви DC I CD (від слів decoder i coder відповідно). Робота дешифратора описується системою логічних рівнянь складених на основі таблиці істинності:
Складаємо рівняння виходів:
За заданими рівняннями складається функціональна схема дешифратора. Шифратор перетворює код “1 із N” в двійковий код, тобто виконує операцію, обернену до дешифратора. При подачі на один із входів шифратора сигналу “лог. 1” на виході формується двійковий код, що відповідає номеру входу, на який подано сигнал “лог. 1”. Робота шифратора описується системою логічних рівнянь складених на основі таблиці істинності:
Складаємо рівняння виходів:
Рівняння переводимо до заданого базису і складаємо функціональну схему шифратора. Приклад виконання завдання №3. Записати логічне рівняння дешифратора, на виході якого буде “лог. 1” тільки при заданих вхідних адресах 126, 127. Задані адреси в вісімковій системі числення: 126, 127. Переведемо адреси в двійкову систему числення. 001 010 110, 001 010 111 Запишемо логічні рівняння:
Виразимо через
Запишемо
Одержані рівняння необхідно перевести в заданий базис і побудувати функціональну схему (рис. 1).
Рис. 1. Функціональна схема шифратора.
|

 , де
, де  – кількість входів.
– кількість входів. .
. ,
,  ,
,  ,
,  . Числу 0101 в двійковому коді відповідає число 5 в десятковому коді, тобто при вказаній комбінації вхідних змінних
. Числу 0101 в двійковому коді відповідає число 5 в десятковому коді, тобто при вказаній комбінації вхідних змінних 




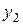

 ;
;  ;
;  ;
;  .
.
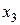
 ;
; .
. ,
, .
. спільну частину:
спільну частину: .
.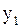 і
і  через
через  ;
; .
.



