Второй замечательный предел
Доказательство второго замечательного предела: Доказательство для натуральных значений x
По формуле бинома Ньютона: Полагая
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:
Поэтому Итак, последовательность ограничена сверху, при этом Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность
1. Пусть Отсюда следует:
Если
По признаку (о пределе промежуточной функции) существования пределов 2. Пусть
Из двух этих случаев вытекает, что
|

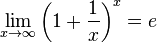 или
или 
 Докажем вначале теорему для случая последовательности
Докажем вначале теорему для случая последовательности 

 , получим:
, получим:
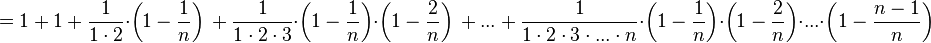 (1)
(1) убывает, поэтому величины
убывает, поэтому величины  возрастают. Поэтому последовательность
возрастают. Поэтому последовательность  — возрастающая, при этом
— возрастающая, при этом (2).
(2).
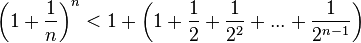 .
. .
. (3).
(3). выполняются неравенства (2) и (3):
выполняются неравенства (2) и (3):  .
. монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.
монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е. 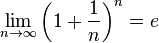

 . Рассмотрим два случая:
. Рассмотрим два случая: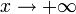 . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами:  , где
, где  — это целая часть x.
— это целая часть x.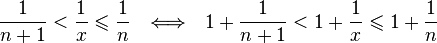 , поэтому
, поэтому .
.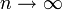 . Поэтому, согласно пределу
. Поэтому, согласно пределу 
 .
. .
. . Сделаем подстановку − x = t, тогда
. Сделаем подстановку − x = t, тогда
 .
.


