Следствия
1. 2. 3. 4. 5. 6. Доказательства следствий 1. 2. 3. 4. 5. 6. 8.Непрерывность функции. Точки разрыва 1-го и 2~гo рода. Функция у = f (х) называется непрерывной в точке х0, если в этой точке бесконечно малому приращению аргумента х-х0= х соответствует бесконечно малое приращение функции
lim y = lim [ f (х0 + х) – f (х0)] = 0. Этому определению равносильно следующее: Функция f (х) называется непрерывной в точке х0, если при х—> х0 предел функции существует и равен ее частному значению в этой точке, т. е. если lim f(х) = f (x0). x->х0
Для непрерывности функции f(х) в точке х0 необходимо и достаточно выполнение следующих условий: 1)функция должна быть определена в некотором интервале, содержащем точку х0.(т. е. в самой точке х0 и вблизи этой точки); 2) функция должна иметь одинаковые односторонние пределы lim f (х) = lim f (x); x->х0 -0 x->х0 +0 3) эти односторонние пределы должны быть равны f (x0). Функция f (x) называется разрывной в точке х0, если она определена в сколь угодно близких точках, но в самой точке х0 не удовлетворяет хотя бы одному из условий непрерывности. Разрыв функции f(х) в точке х0 называется конечным, или 1-го рода, если существуют конечные односторонние пределы lim f(x) и lim f(х). x-> х0 -0 x-> х0 +0 Все другие случаи разрыва функции называются разрывами- 2-го-рода; в частности, если хотя бы один из указанных односторонних пределов окажется бесконечным, то и разрыв функции называется бесконечным. Скачком функции f(х) в точке разрыва х0 называется разность ее односторонних пределов lim f(x) и lim f(х) если они различны. x-> х0 -0 x-> х0 +0 Если точка х0 является левой или правой границей области определения функции f(х), то следует рассматривать значения функции соответственно только справа или только слева от этой точки и в самой точке. При этом: 1) если граничная точка х0 входит в область определения функции, то она будет точкой непрерывности или точкой разрыва функции, смотря по тому, будет ли предел функции при х —>х0 изнутри ее области определения равен или не равен f(х0); 2) если граничная точка х0 не входит в область определения функции, то она является точкой разрыва функции. Функция называется непрерывной в некотором интервале, если она непрерывна во всех точках этого интервала.
|

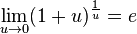

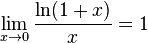

 для
для  ,
, 





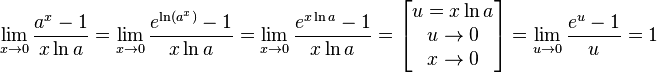

 у—у0 = у, т. е. если
у—у0 = у, т. е. если


