Частной производной от функции  по независимой переменной
по независимой переменной  называется производная
называется производная
 , вычисленная при постоянном
, вычисленная при постоянном 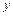 .
.
Частной производной по y называется производная 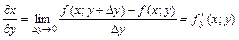 , вычисленная при постоянном
, вычисленная при постоянном  . Для частных производных справедливы обычные правила и формулы дифференцирования.
. Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1.  .
.
Рассматривая  как постоянную величину
как постоянную величину  , получим
, получим  .
.
Рассматривая  как постоянную величину
как постоянную величину  , получим
, получим  .
.
Пример 2. 
 ;
;  ;
;
 ;
;  .
.
Полным приращением функции  в точке
в точке  называется разность
называется разность  , где
, где  и
и  произвольные приращения аргументов. Функция
произвольные приращения аргументов. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если в этой точке полное приращение можно представить в виде
, если в этой точке полное приращение можно представить в виде 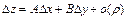 , где
, где 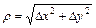 .
.
Полным дифференциалом функции  называется главная часть полного приращения
называется главная часть полного приращения  , линейная относительно приращений аргументов
, линейная относительно приращений аргументов  и
и  , то есть
, то есть  .
.
Полный дифференциал функции  вычисляется по формуле
вычисляется по формуле  .
.
Для функции трех переменных  .
.
При достаточно малом 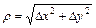 для дифференцируемой функции
для дифференцируемой функции  справедливы приближенные равенства
справедливы приближенные равенства 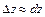 ;
; 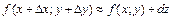 , которые применяются для приближенного вычисления значения функции
, которые применяются для приближенного вычисления значения функции
 . (*)
. (*)
Пример 3. Вычислить приближенное значение:  .
.
Решение. Полагая, что  есть частное значение функции
есть частное значение функции  в точке
в точке  и что вспомогательная точка будет
и что вспомогательная точка будет  , получим
, получим 
 ;
;  ;
;  ;
;  .
.
Подставляя в формулу (*), найдем:
 .
.
Частными производными второго порядка от функции  называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Обозначения частных производных второго порядка:
 ;
;  ;
;
 ;
;  .
.
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны:  .
.
Дифференциалом второго порядка от функции  называется дифференциал от ее полного дифференциала, то есть
называется дифференциал от ее полного дифференциала, то есть  . Если
. Если  и
и 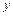 – независимые переменные и функция
– независимые переменные и функция  имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле
имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле  .
.
Пример 4.  . Найти
. Найти  ,
,  ,
,  .
.
Решение. Найдем частные производные:  ;
; 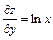 . Дифференцируя повторно, получим
. Дифференцируя повторно, получим  ;
;
 ;
;  .
.

 по независимой переменной
по независимой переменной  называется производная
называется производная , вычисленная при постоянном
, вычисленная при постоянном 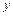 .
.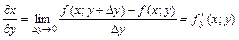 , вычисленная при постоянном
, вычисленная при постоянном  .
. , получим
, получим  .
. , получим
, получим  .
.
 ;
;  ;
; ;
;  .
. называется разность
называется разность  , где
, где  и
и  произвольные приращения аргументов. Функция
произвольные приращения аргументов. Функция  , если в этой точке полное приращение можно представить в виде
, если в этой точке полное приращение можно представить в виде 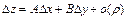 , где
, где 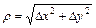 .
. , линейная относительно приращений аргументов
, линейная относительно приращений аргументов  .
. .
. .
.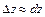 ;
; 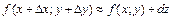 , которые применяются для приближенного вычисления значения функции
, которые применяются для приближенного вычисления значения функции . (*)
. (*) .
. в точке
в точке  и что вспомогательная точка будет
и что вспомогательная точка будет  , получим
, получим 
 ;
;  ;
;  ;
;  .
. .
. ;
;  ;
; ;
;  .
. .
. . Если
. Если  имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле
имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле  .
. . Найти
. Найти  ,
,  ,
,  .
. ;
; 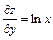 . Дифференцируя повторно, получим
. Дифференцируя повторно, получим  ;
; ;
;  .
.


