Интегральные суммы. Определенный интеграл. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница.
Множество T = { xi } точек отрезка [ a, b ], таких, что a = x0 < x1 < x2 < …… < xT–1 < xT= b называется разбиением отрезка [ a, b ]. Обозначим D xk длину отрезка [ xk-1 , xk ]. Тогда максимальное значение D xk называется мелкостью разбиения T. Если множество Т* включает в себя множество Т, то говорят, что разбиение Т* следует за разбиением Т; или что разбиение Т* вписано в разбиение Т. Для двух разбиений Т и Т* всегда найдется разбиение, вписанное и в Т, и в Т*. ОПРЕДЕЛЕНИЕ. Если функция f (x) задана всюду на отрезке [ a, b ] и задано разбиение Т, то всякая сумма:
называется интегральной суммой Римана функции f. ОПРЕДЕЛЕНИЕ. Функция f (x) называется интегрируемой по Риману на отрезке [ a, b ], если для любой последовательности разбиений Тn отрезка [ a, b ], мелкость которых стремится к нулю; и для любого набора точек x k последовательность интегральных сумм s Т n имеет один и тот же предел. Предел последовательности интегральных сумм называют (определенным) интегралом Римана функции f на отрезке [ a, b ] и обозначается В интеграле Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a). Пусть f (x) непрерывна на [ a; b ], g (t) имеет непрерывную производную на [α; β],
Если функции u (x) и v (x) имеют на [ a; b ] непрерывные производные, то справедлива формула интегрирования по частям:
|


 .
. Пусть функция f (x) непрерывна на [ a; b ], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Пусть функция f (x) непрерывна на [ a; b ], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
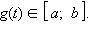 Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:
Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле: