При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
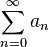
существует такое число  ,
,  , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство
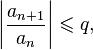
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме
Если существует предел
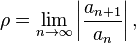
то рассматриваемый ряд абсолютно сходится если  , а если
, а если  — расходится.
— расходится.
Замечание. Если  , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
-
 , тогда существует
, тогда существует  , существует
, существует  , для любого
, для любого  .
.
Ряд из  сходится (как геометрическая прогрессия). Значит, ряд из
сходится (как геометрическая прогрессия). Значит, ряд из  сходится (по признаку сравнения).
сходится (по признаку сравнения). -
 , тогда существует
, тогда существует  .
. 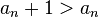 для любого
для любого  . Тогда
. Тогда  не стремится к нулю и ряд расходится.
не стремится к нулю и ряд расходится.
Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на 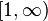 , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.
Пусть для функции f(x) выполняется:
-
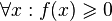 (функция принимает неотрицательные значения)
(функция принимает неотрицательные значения) -
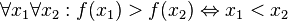 (функция монотонно убывает)
(функция монотонно убывает) -
 (соответствие функции ряду)
(соответствие функции ряду)
Тогда ряд  и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Набросок доказательства
- Построим на графике f(x) ступенчатые фигуры как показано на рисунке
- Площадь большей фигуры равна

- Площадь меньшей фигуры равна

- Площадь криволинейной трапеции под графиком функции равна

- Получаем

- Далее доказывается с помощью критерия сходимости знакоположительных рядов.

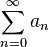
 ,
,  , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство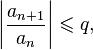
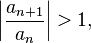
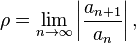
 , а если
, а если  — расходится.
— расходится. , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда. , тогда существует
, тогда существует  , существует
, существует  , для любого
, для любого  .
. сходится (как геометрическая прогрессия). Значит, ряд из
сходится (как геометрическая прогрессия). Значит, ряд из  сходится (по признаку сравнения).
сходится (по признаку сравнения). , тогда существует
, тогда существует  .
. 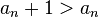 для любого
для любого  . Тогда
. Тогда 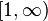 , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.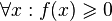 (функция принимает неотрицательные значения)
(функция принимает неотрицательные значения)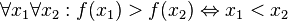 (функция монотонно убывает)
(функция монотонно убывает) (соответствие функции ряду)
(соответствие функции ряду) и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.






