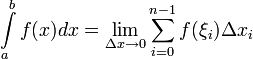Методы интегрирования. Непосредственное интегрирование. Метод подстановки. Интегрирование по частям. Определенные и несобственные интегралы
Непосредственное интегрирование Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой. Пусть требуется вычислить интеграл Тогда
Интегрирование по частям — применение следующей формулы для интегрирования:
Или:
где Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала). Пусть Определённым интегралом от функции
Если существует указанный предел, то функция Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
|

 Сделаем подстановку
Сделаем подстановку  где
где  — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную. и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
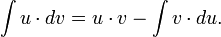


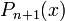 — многочлен
— многочлен 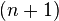 -ой степени.
-ой степени. определена на
определена на  . Разобьём
. Разобьём  . Тогда говорят, что произведено разбиение
. Тогда говорят, что произведено разбиение 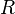 отрезка
отрезка  Далее выберем произвольную точку
Далее выберем произвольную точку  ,
,  ,
, , если он существует независимо от разбиения
, если он существует независимо от разбиения  , то есть
, то есть