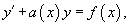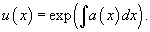Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
Умножение левой части уравнения на интегрирующий множитель u (x) преобразует ее в производную произведения y (x) u (x). Общее решение диффференциального уравнения выражается в виде:
где C − произвольная постоянная. Метод вариации постоянной Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C (x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C (x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату. Задача Коши Если, кроме дифференциального уравнения, задано также начальное условие в форме y (x 0) = y 0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y (x 0) = y 0.
|