Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:

в котором коэффициенты  берутся из некоторого кольца
берутся из некоторого кольца 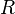 .
.
Пространство степенных рядов с одной переменной и коэффициентами из 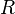 обозначается
обозначается  . Пространство
. Пространство  имеет структуру дифференциальной алгебры над кольцом
имеет структуру дифференциальной алгебры над кольцом 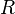 (коммутативной, целостной, с единицей, если таково же кольцо
(коммутативной, целостной, с единицей, если таково же кольцо 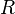 ). Оно часто используется в математике ввиду того, что в нём легко представимы и разрешимы формальные дифференциально-алгебраические и даже функциональные соотношения (см. метод производящих функций). При его использовании эти соотношения превращаются в алгебраические уравнения на коэффициенты рядов. Если они разрешаются, говорят о получении формального решения исходной задачи в виде формального степенного ряда.
). Оно часто используется в математике ввиду того, что в нём легко представимы и разрешимы формальные дифференциально-алгебраические и даже функциональные соотношения (см. метод производящих функций). При его использовании эти соотношения превращаются в алгебраические уравнения на коэффициенты рядов. Если они разрешаются, говорят о получении формального решения исходной задачи в виде формального степенного ряда.
В  определены операции сложения, умножения, формального дифференцирования и формальной суперпозиции. Пусть
определены операции сложения, умножения, формального дифференцирования и формальной суперпозиции. Пусть
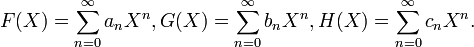
Тогда:

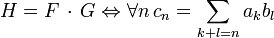
 (при этом необходимо, чтобы соблюдалось
(при этом необходимо, чтобы соблюдалось 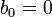 )
)
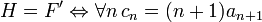
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
- Первая теорема Абеля: Пусть ряд
 сходится в точке
сходится в точке  . Тогда этот ряд сходится абсолютно в круге
. Тогда этот ряд сходится абсолютно в круге  и равномерно по
и равномерно по  на любом компактном подмножестве этого круга.
на любом компактном подмножестве этого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при  , он расходится при всех
, он расходится при всех  , таких что
, таких что 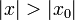 . Из первой теоремы Абеля также следует, что существует такой радиус круга
. Из первой теоремы Абеля также следует, что существует такой радиус круга 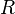 (возможно, нулевой или бесконечный), что при
(возможно, нулевой или бесконечный), что при  ряд сходится абсолютно (и равномерно по
ряд сходится абсолютно (и равномерно по  на компактных подмножествах круга
на компактных подмножествах круга  ), а при
), а при  — расходится. Это значение
— расходится. Это значение 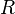 называется радиусом сходимости ряда, а круг
называется радиусом сходимости ряда, а круг  — кругом сходимости.
— кругом сходимости.
- Формула Коши-Адамара: Значение радиуса сходимости степенного ряда (если верхний предел существует и положителен, теорема Адамара о степенном ряде) может быть вычислено по формуле:
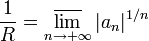
(По поводу определения верхнего предела  см. статью «Частичный предел последовательности».)
см. статью «Частичный предел последовательности».)
Пусть  и
и 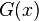 — два степенных ряда с радиусами сходимости
— два степенных ряда с радиусами сходимости  и
и  . Тогда
. Тогда



Если у ряда 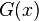 свободный член нулевой, тогда
свободный член нулевой, тогда
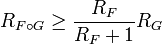
Вопрос о сходимости ряда в точках границы  круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
- Признак Д’Аламбера: Если при
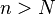 и
и  выполнено неравенство
выполнено неравенство

тогда степенной ряд  сходится во всех точках окружности
сходится во всех точках окружности  абсолютно и равномерно по
абсолютно и равномерно по  .
.
- Признак Дирихле: Если все коэффициенты степенного ряда
 положительны и последовательность
положительны и последовательность  монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности
монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности 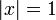 , кроме, быть может, точки
, кроме, быть может, точки 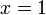 .
. - Вторая теорема Абеля: Пусть степенной ряд сходится в точке
 . Тогда он сходится равномерно по
. Тогда он сходится равномерно по  на отрезке, соединяющем точки
на отрезке, соединяющем точки  и
и  .
.
Сумма степенного ряда как функция комплексного параметра  является предметом изучения теории аналитических функций.
является предметом изучения теории аналитических функций.


 берутся из некоторого кольца
берутся из некоторого кольца 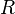 .
. . Пространство
. Пространство 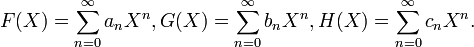

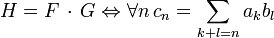
 (при этом необходимо, чтобы соблюдалось
(при этом необходимо, чтобы соблюдалось 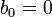 )
)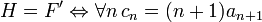
 сходится в точке
сходится в точке  . Тогда этот ряд сходится абсолютно в круге
. Тогда этот ряд сходится абсолютно в круге  и равномерно по
и равномерно по  на любом компактном подмножестве этого круга.
на любом компактном подмножестве этого круга. , он расходится при всех
, он расходится при всех 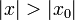 . Из первой теоремы Абеля также следует, что существует такой радиус круга
. Из первой теоремы Абеля также следует, что существует такой радиус круга  ряд сходится абсолютно (и равномерно по
ряд сходится абсолютно (и равномерно по  — расходится. Это значение
— расходится. Это значение 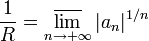
 см. статью «Частичный предел последовательности».)
см. статью «Частичный предел последовательности».) и
и  — два степенных ряда с радиусами сходимости
— два степенных ряда с радиусами сходимости  и
и  . Тогда
. Тогда


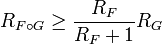
 круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости: и
и  выполнено неравенство
выполнено неравенство
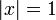 , кроме, быть может, точки
, кроме, быть может, точки 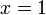 .
. и
и 


