Метод неопределенных коэффициентов
Правая часть f (x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α; в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α; в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Числовые ряды. Основные понятия и определения
|
Числа 
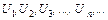называются, соответственно, первым, вторым, n –м … членами ряда. 
называется также общим членом ряда. Ряд считается заданным, если известен общий член ряда 
.
Определение: Сумма n первых членов ряда называется n –й частичной суммой ряда: 
.
Определение: Если существует конечный предел 
, то его называют суммой ряда, а ряд при этом называется сходящимся. Если 
не существует или равен бесконечности, то ряд называется расходящимся.
В школьном курсе математики рассматриваются такие ряды, как натуральный ряд чисел и бесконечная геометрическая прогрессия: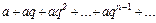 
. Известно, что при 
сумма бесконечно убывающей геометрической прогрессии равна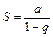 
, то есть бесконечно убывающая геометрическая прогрессия является сходящимся числовым рядом.
и 
– n –е частичные суммы рядов (1) и (2) соответственно.
и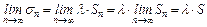 
, следовательно, ряд (2) сходится и имеет сумму 
соответственно, то ряды
соответственно.
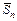и 
,
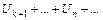
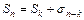, где k –некоторое число, не зависящее от n. Пусть ряд (1) сходится и имеет сумму S, то есть 
. Тогда
,
– 
–я частичная сумма ряда (5).
, то есть 
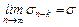. Тогда 
что означает сходимость ряда (1). Аналогично доказываются случаи рассходимости. Предоставляем сделать это самостоятельно.
.
,
, тогда 
, что и требовалось доказать.
, то ряд расходится.
. В качестве примера рассмотрим ряд 
.
. Рассмотрим 
. Так как 
то 
, то есть 
, что означает расходимость рассматриваемого ряда.
