Матрицы. Основные определения. Действия над матрицами. Их свойства.
Матрицы. Основные определения. Действия над матрицами. Их свойства. Пусть m и n два произвольных натуральных числа. Матрицей размера m на n (записывается так Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами: 1. Сложение матриц Сложение: операция сложения матрицы вводится только для матриц одинаковых размеров. Суммой двух матриц тогда Аналогично определяется разность матриц.
2. Умножение матрицы на число Произведением матрицы Примечание: матрица Операции сложения и умножения матрицы на число обладают следующими свойствами: 1) 2) 3) 4) 5) 6) 7) 8)
3. Умножение матрицы на матрицу Мы будем всегда говорить, что умножение двух матриц возможно, если число столбцов первой матрицы равно числу строк второй матрицы: где Например: В общем случае Продолжим перечисление свойств (см. п. 2.3.2):
9) 10) 11) 12) 13) 14) 4. Элементарные преобразования матриц К элементарным преобразованиям матриц относят: – перестановку местами двух параллельных рядов матрицы; – умножение всех элементов ряда матрицы на число, отличное от нуля; – прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Две матрицы При получении элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
5. Определители матриц и их свойства Квадратную матрицу Вычисление определителя: т. е. правило: т. е. Правило треугольника (или Саррюса):
Отметим следующие свойства определителей: – определители не изменяются, если его строки заменить столбцами и наоборот (строки и столбцы это ряд определителя); – при перестановке двух параллельных рядов определитель меняет знак; – определитель, имеющий два одинаковых ряда, равен нулю; – общий множитель элементов какого-либо рода определителя можно вынести за знак определителя; – если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму соответственных определителей; – определитель не изменяется, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число; Дальнейшие свойства связаны с понятием минора и алгебраического дополнения. 2. Определители 2-го и 3-го порядков. Вычисление. Свойства. Определители n-ГО порядка (n>>3). Вычисление. Определителем называется число, записанное в виде квадратной таблицы:
Таблица ограничивается слева и справа вертикальными линиями, Главная диагональ определителя содержит элементы Порядком определителя называется число строк (столбцов) квадратной таблицы. Определитель II порядка вычисляется по формуле: Определитель III порядка можно вычислить по правилу Сарруса:
Основные свойства определителей: 1.1. Значение определителя не изменится, если: - строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов; - все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки. Такие действия с элементами определителя называются элементарными преобразованиями. 1.2. Определитель меняет знак на противоположный, если две каких-либо строки поменять местами. 1.3. Определитель равен нулю, если: - все элементы какой-либо строки равны нулю; - соответствующие элементы каких-либо двух строк равны; - соответствующие элементы каких-либо двух строк пропорциональны. Определителем или детерминантом n-го порядка называется число записываемое в виде
и вычисляемым по данным числам
распространенная на всевозможные различные перестановки Определители Доказательство. а) После замены у определителя соответствующих строк столбцами теперь уже номера строк будут обозначаться вторыми индексами. Например, для определителя третьего порядка (2) будем иметь
В общем случае общий член нового определителя запишется
Упорядочим множители произведения
Нетрудно видеть, что разным перестановкам
б) Поменяем местами, например, первую и третью строки определителя третьего порядка (2). Тогда получим определитель, который обозначим через
так как перестановка Будем говорить, что число в) Умножение на число г) Определитель, у которого элементы какого-либо столбца или строки равны нулю, равен нулю, потому что все его члены, очевидно, равны нулю. д) Определитель равен нулю, если он имеет две одинаковые строки или два одинаковых столбца. Это следует из свойства б) ( Вычеркнем из определителя (9)
называется алгебраическим дополнением или адъюнктом элемента Свойство е) Сумма произведений элементов
Докажем это свойство для определителя третьего порядка в случае третьей строки. Имеем
Сумму (10) называют разложением определителя по элементам
|

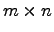 )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
)называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.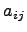 - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом
- элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом и
и 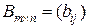 называется матрица
называется матрица 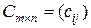 такая, что
такая, что 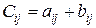
 , например,
, например,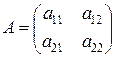 ,
,  ,
, .
. такая, что
такая, что 

 называется противоположной матрице
называется противоположной матрице  .
. ;
; ;
;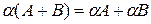 ;
; ;
;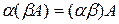 ;
; ;
; ;
; .
. ;
; 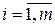 ;
;  ;
;  .
.  ,
, ;
;  .
.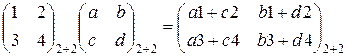 .
. .
. ;
; ;
; ;
; ;
; ;
; .
. называются эквивалентными, т. е.
называются эквивалентными, т. е.  (или
(или 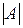 , или
, или  ), называемым определителем или детерминантом.
), называемым определителем или детерминантом. ;
;
 ,
, ;
;

 .
. .
. -называется элементами определителя (
-называется элементами определителя ( 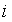 -номер строки,
-номер строки, 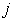 -номер столбца).
-номер столбца). , противоположная диагональ называется побочной.
, противоположная диагональ называется побочной.
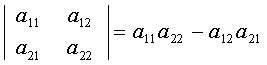

 (9)
(9) (действительным или комплексным) — элементам определителя – по следующему закону:
(действительным или комплексным) — элементам определителя – по следующему закону:  есть сумма
есть сумма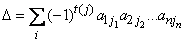 ,
, из чисел 1, 2, …,
из чисел 1, 2, …,  . Число
. Число  равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 1, 2, …,
равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 1, 2, …,  называется членом определителя.
называется членом определителя. .
. .
. по первому индексу, т. е. мы переходим от перестановки
по первому индексу, т. е. мы переходим от перестановки  и число
и число  будет той же четности, что и число
будет той же четности, что и число  .
.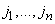 соответствуют разные перестановки
соответствуют разные перестановки  . Но тогда
. Но тогда .
.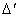 , он будет равен
, он будет равен ,
, отличается от перестановки
отличается от перестановки  одной транспозицией.
одной транспозицией. умножается, на строку (столбец) определителя, если на самом деле
умножается, на строку (столбец) определителя, если на самом деле  ,
,  , откуда
, откуда  ).
). -ю строку и
-ю строку и 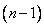 -го порядка
-го порядка  , называемый минором элемента
, называемый минором элемента 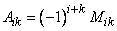
 , (10)
, (10) (10')
(10')




