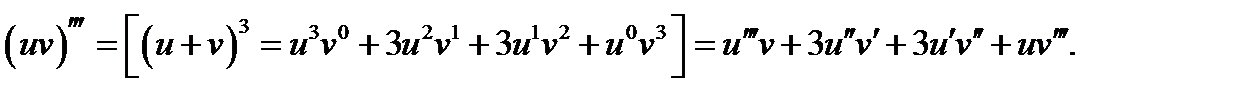Производные и дифференциалы высших порядков
Производная если известна производная Аналогично определяются дифференциалы высшего порядка. Именно: если известен дифференциал Имеем
Нетрудно доказать следующее утверждение. Теорема 1. В области определения выписанных ниже функций справедливы равенства:
Производные
Формула Лейбница. Если функции
Здесь:
|
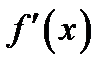есть сама функция от 
поэтому можно взять от нее производную. Полученная таким образом функция (если она существует) называется второй производной от функции 
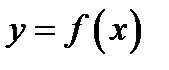и обозначается 
И вообще:
(
порядка), то производная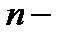 
го порядка определяется так: 
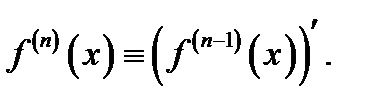При этом функция 
называется 
раз дифференцируемой в точке 
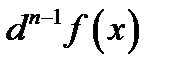
го порядка определяется так: 
при этом дифференциал 
независимой переменной и все его степени 
считаются постоянными дифференцирования.
И вообще, справедливо утверждение: если функция 
то
порядка являются линейными операциями, т.е. 
Производная 
вычисляется довольно сложно.
дифференцируемы 
раз в точке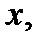 
то имеет место равенство
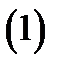
число сочетаний из 
элементов по 
нулевая производная функции 
совпадает с ней самой: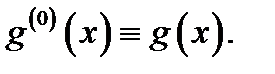 
Легко видеть, что формула (1) напоминает формулу бинома Ньютона; только в ней вместо произведения степеней 
стоит произведение производных 
Учитывая это, легко записать, например, третью производную от произведения:
