Производная сложной и обратной функций и функции, заданной параметрически
Приведем без доказательства некоторые утверждения, связанные с производными. Теорема 5. Пусть сложная функция 1. функция 2. функция Тогда сложная функция
Напомним следующие понятия: а) Функция
При этом функция Очевидно, имеют место тождества:
Заметим, что все строго монотонные на множестве б) Говорят, что функция Теорема 6. Пусть функция Теорема 7. Пусть функция 1) функции 2) Тогда функция
|
определена в точке 
и некоторой ее окрестност и пусть выполнены условия:
дифференцируема в точке 
дифференцируема в соответствующей точке 
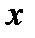и имеет место равенство
называется обратимой на множестве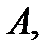 
если
сопоставляющая каждому 
элемент 
такой, что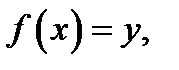 
называется функцией, обратной к 
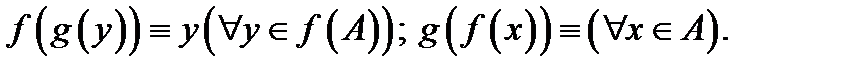
функции обратимы на 
задана параметрически уравнениями 
если функция 
обратима на отрезке 
В этом случае 
где 
функция, обратная к функции 
в некоторой окрестности точки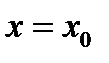 
имеет обратную функцию 
Пусть, кроме того, функция 
дифференцируема в точке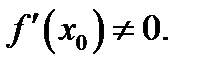 
Тогда обратная функция 
дифференцируема в соответствующей точке 
и имеет место равенство 
и пусть выполнены условия: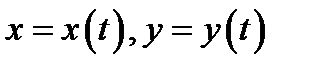
дифференцируемы в фиксированной точке 
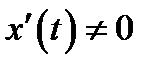в рассматриваемой точке 
и имеет место равенство
