Вычисление определителей
Значение определителя 2-го порядка легко вычисляется по определению используя формулу (2). Для нахождения значения определителя 3-го порядка можно использовать формулу (3). Определители более высоких порядков в принципе тоже можно было бы вычислять по определению, однако это требует очень больших усилий. Чаще поступают следующим образом: определитель n-го порядка сводят к опреде-лителям (n-1)-го порядка, последние - к определителям (n-2)-го порядка и т. д., до тех пор, пока, наконец, не получат определители 3-го или 2-го порядка. В основе этого принципа "постепенного понижения порядка" лежит теорема разложения: определитель n-го порядка D записывается в виде суммы определителей порядка (n-1) ("раскладывается по элементам i-й строки или j-го столбца"); к каждому из этих определителей порядка n-1 вновь может быть применена теорема разложения. Если все элементы аik i-й строки определителя D, кроме одного, равны нулю, то сумма, полученная после применения теоремы разложения, содержит только одно отличное от нуля слагаемое. Таким образом, вычисления существенно упрощаются, если перед разложением определителя по элементам i-й строки как можно больше из них будут превращены в нули. Это становится возможным благодаря применению свойств определителей (особенно свойства 5). Еще удобнее оказывается вычисление определителя, если, применяя его свойства, можно преобразовать его так, чтобы все элементы, стоящие слева и ниже диагонали а11, а22,..., аnn были равны нулю. Как легко понять на основании теоремы разложения, значение определителя получается тогда просто как произведение членов, стоящих на главной диагонали: D = a11a22...аnn. 4.Правило Крамера (вывод формул…)
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат. Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Далее рассмотрим коэффициенты при x2: что и
Аналогично выводятся равенства Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
|

 Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных, называется определителем системы.
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных, называется определителем системы.


 Сложим эти уравнения:
Сложим эти уравнения: Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
 Аналогично можно показать,
Аналогично можно показать, Наконец несложно заметить, что
Наконец несложно заметить, что Таким образом, получаем равенство:
Таким образом, получаем равенство: Следовательно,
Следовательно, и
и 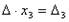 , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.


