Исследование систем m линейных уравнений c n неизвестными. Метод Гаусса.
Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая. Условие совместности системы линейных уравнений даёт следующая теорема Теорема 6.1 (Кронекера–Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:
Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем. Теорема 6.2. Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой Теорема 6.3. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой. Таким образом, из сформулированных теорем вытекает способ исследования систем линейных алгебраических уравнений. Пусть n – количество неизвестных, 1) при 2) при Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Метод Гаусса - метод последовательного исключения переменных. С помощью элементарных преобразований строк расширенной матрицы D системы матрицу A системы приводят к ступенчатому виду:
Если 1) при r = n исходная система равносильна системе: имеющей единственное решение (сначала находим из последнего уравнения 2) при r < n исходная система равносильна системе: имеющей бесчисленное множество решений (
|

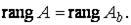
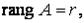
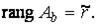 Тогда:
Тогда: система несовместна;
система несовместна;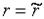 система совместна, причём, если
система совместна, причём, если 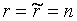 , система
, система  , система неопределённая.
, система неопределённая.
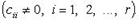 Если среди чисел
Если среди чисел 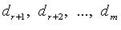 есть отличные от нуля, система несовместна.
есть отличные от нуля, система несовместна.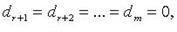 то:
то: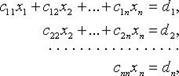
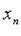 , из предпоследнего
, из предпоследнего 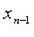 и т. д.);
и т. д.);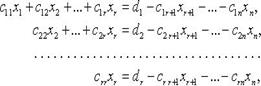
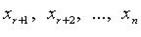 - свободные переменные).
- свободные переменные).


