Система линейных однородны уравнений. Теорема о ненулевых решениях таких систем (доказать).
Запишем однородную систему линейных уравнений. Согласно общей теории, если r(A)=n, то единственным является тривиальное (нулевое) решение. Если же r(A)<n, то решений бесконечно много, и все они, кроме одного, нетривиальные (ненулевые). Теорема 7.1 (о нетривиальных (ненулевых) решениях однородной системы) Однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю. Доказательство: По теореме Крамера det(A) ≠ 0 тогда и только тогда, когда система с квадратной матрицей имеет единственное решение (т.е. векторы – столбцы системы (7.1) – линейно зависимы). В случае если задана система линейных однородных уравнений, это решение – тривиальное (0,0,…0). Значит, нетривиальные решения имеются тогда и только тогда, когда det(A)=0 (т.е. решений системы бесконечное множество). векторов (если r(A)=r): Ниже черты расположен минор порядка (n-r), отличный от нуля, следовательно r(Г)= (n-r),следовательно (n-r) столбцов матрицы Г линейно независимы. Следовательно, вектора qr+1,...,qn – линейно независимы, т.е. эти вектора образуют базис подпространства. Всякая линейно независимая система (n-r) решений системы линейных однородных уравнений называется фундаментальной системой решений.
|

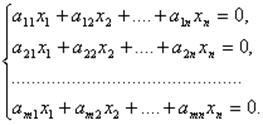 РИС. 7.1
РИС. 7.1 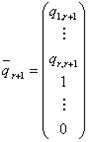 …,
…, 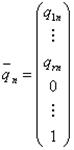 РИС. 7.2
РИС. 7.2



