Векторное произведение. Координаты вектора векторного произведения. Его свойства. Условия колинеарности.
15.Приложение векторного произведения: площадь треугольника в пространстве и на плоскости через координаты его вершин. Векторы на плоскости и в пространстве Вектор — это направленный отрезок. Его длиной считают длину отрезка. Если даны две точки M1 (x1, y1, z1) и M2 (x2, y2, z2), то вектор Расстояние между двумя точками — это длина отрезка М1М2 или длина вектора n: Если даны два вектора 1.Длины векторов: 2.Сумма векторов: Суммой двух векторов a и b является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма); или вектор, соединяющий начало первого вектора с концом последнего — по правилу треугольника. Суммой трех векторов a, b, c называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда). 3.Разность векторов: 4.Умножение вектора на число (скаляр): Векторы t и b называются коллинеарными, т.е. лежат на параллельных прямых или на одной прямой. Пропорциональные координаты — условие коллинеарности векторов. 5.Скалярное произведение векторов: Если скалярное произведение равно нулю, то векторы перпендикулярны. 6.Угол между векторами a и b, точнее его косинус: 7.Векторное произведение векторов: где S — площадь параллелограмма, построенного на векторах a, b. Если, то данные векторы коллинеарные (параллельны прямой). 8.Смешанное произведение векторов
Если, то данные векторы компланарные (принадлежат плоскости или параллельны ей).
Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е..
|

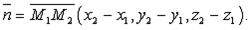

 и
и  , то:
, то:

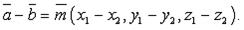




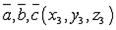
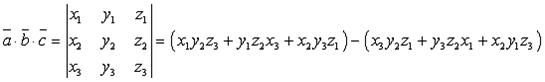
 Три ненулевых вектора a, b, cкомпланарны, когда один из них выражается через два других, т.е., где n, m — числа.
Три ненулевых вектора a, b, cкомпланарны, когда один из них выражается через два других, т.е., где n, m — числа.


