Различные уравнения прямой на плоскости(наклонной,через две точки, общее, каноническое,параметрическое).
Пусть прямая проходит через точку М0 (x0,y0) перпендикулярно вектору n = {A,B}. Тогда вектор А(х – х0) + В(у – у0) = 0 - уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.Замечание. Вектор n называется нормалью к прямой. Преобразуем уравнение к виду: Ах + Ву + (-Ах0 – Ву0) = 0. Обозначив -Ах0 – Ву0 = С, получим общее уравнение прямой: Ах + Ву + С = 0.
и из уравнения Обозначив за t значения равных дробей, стоящих в левой и правой частях уравнения, можно преобразовать это уравнение к виду: x = x0 + lt, y = y0 + mt - параметрические уравнения прямой. Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k – тангенс угла, образованного прямой и осью Ох, и записать уравнение прямой в виде: у = kx + b - уравнение прямой с угловым коэффициентом. Действительно, все точки прямой l1, параллельной l и проходящей через начало координат, удовлетворяют уравнению у = kх, а ординаты соответствующих точек на прямой l отличаются от них на постоянную величину b. Неполные уравнения прямой. Уравнение Ах + Ву + С = 0. называется полным, если коэффициенты А,В и С не равны нулю, и неполным, если хотя бы одно из этих чисел равно нулю. Рассмотрим возможные виды неполных уравнений прямой. 1) С = 0 - прямая Ах + Ву = 0 проходит через начало координат. 2) В = 0 - прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой {A,0} перпендикулярна оси Оу). 3) А = 0 - прямая Ву + С = 0 параллельна оси Ох. 4) В=С=0 – уравнение Ах = 0 определяет ось Оу. 5) А=С=0 – уравнение Ву = 0 определяет ось Ох. Таким образом, прямая, задаваемая полным уравнением, не проходит через начало координат и не параллельна координатным осям. Преобразуем полное уравнение прямой следующим образом: Ах + Ву + С = 0 |:(-C), Где 19. Пусть на плоскости зафиксирована прямоугольная декартоваHYPERLINK "http://www.cleverstudents.ru/cartesian_rectangular_coordinates.html" систему координат Oxy. Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид Уравнение прямой в отрезках не случайно получило такое название - абсолютные величины чисел a и b равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат. Поясним этот момент. Мы знаем, что координаты любой точки прямой удовлетворяют уравнению этой прямой. Тогда отчетливо видно, что прямая, заданная уравнением прямой в отрезках, проходит через точки Изобразим схематический чертеж, поясняющий все вышесказанное. На нем показано расположение прямых относительно фиксированной прямоугольной системы координат Oxy в зависимости от значений чисел a и b в уравнении прямой в отрезках.
Теперь стало понятно, что уравнение прямой в отрезках позволяет легко производить построение этой прямой линии в прямоугольной системе координат Oxy. Чтобы построить прямую линию, которая задана уравнением прямой в отрезках вида Нормальное уравнение прямой – описание и пример. Выведем нормальное уравнение прямой. Пусть на плоскости зафиксирована прямоугольная декартоваHYPERLINK "http://www.cleverstudents.ru/cartesian_rectangular_coordinates.html" система координат Oxy. Зададим прямую в этой системе координат, указав точку, через которую она проходит, и нормальный вектор прямой. В качестве нормального вектора нашей прямой возьмем вектор единичной длины Получим уравнение, которое задает эту прямую линию. Очевидно, что точка
Полученное уравнение вида Очевидно, нормальное уравнение прямой представляет собой общее уравнение прямой вида Из вывода нормального уравнения прямой виден его геометрический смысл: нормальное уравнение прямой вида Для примера приведем нормальное уравнение прямой
20.
|

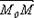 , где М(х,у) – произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению
, где М(х,у) – произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению Получим теперь уравнение прямой, проходящей через точку М0 (x0,y0) параллельно вектору q = {l,m}. Так как вектор
Получим теперь уравнение прямой, проходящей через точку М0 (x0,y0) параллельно вектору q = {l,m}. Так как вектор 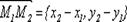 называемому каноническим уравнением прямой. Вектор q при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М1(х1,у1) и М2(х2,у2), ее направляющим вектором можно считать
называемому каноническим уравнением прямой. Вектор q при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М1(х1,у1) и М2(х2,у2), ее направляющим вектором можно считать следует:
следует:  уравнение прямой, проходящей через две заданные точки.
уравнение прямой, проходящей через две заданные точки.

 и
и  равны величинам отрезков, отсекаемых прямой на осях Ох и Оу. Поэтому уравнение
равны величинам отрезков, отсекаемых прямой на осях Ох и Оу. Поэтому уравнение 
 называют уравнением прямой в отрезках.
называют уравнением прямой в отрезках.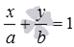 , где a и b - некоторые отличные от нуля действительные числа.
, где a и b - некоторые отличные от нуля действительные числа.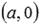 и
и  , так как
, так как  и
и 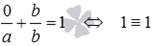 . А точки
. А точки 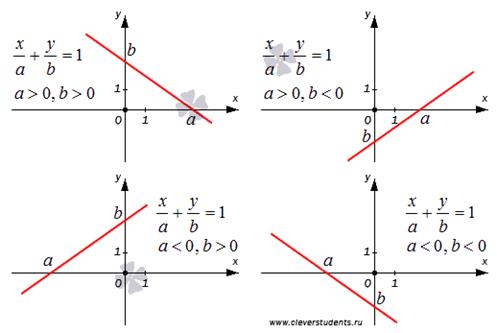
 , с началом в точке O. Его координаты равны соответственно
, с началом в точке O. Его координаты равны соответственно  и
и 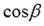 , где
, где  и
и  - углы между вектором
- углы между вектором  . В качестве точки, через которую проходит прямая, возьмем точку А и будем считать, что она находится на расстоянии p единиц (
. В качестве точки, через которую проходит прямая, возьмем точку А и будем считать, что она находится на расстоянии p единиц ( ) от точки O в положительном направлении вектора
) от точки O в положительном направлении вектора  .
.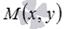 лежит на рассматриваемой прямой тогда и только тогда, когда числовая проекция вектора
лежит на рассматриваемой прямой тогда и только тогда, когда числовая проекция вектора  на направление вектора
на направление вектора  .
.
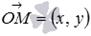 , что было показано в разделе координаты радиус-вектора точки. Тогда из определения скалярного HYPERLINK "http://www.cleverstudents.ru/scalar_product_of_vectors.html"произведения векторов мы получаем равенство
, что было показано в разделе координаты радиус-вектора точки. Тогда из определения скалярного HYPERLINK "http://www.cleverstudents.ru/scalar_product_of_vectors.html"произведения векторов мы получаем равенство 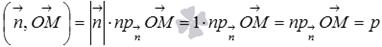 , а это же скалярное произведение в координатной форме имеет вид
, а это же скалярное произведение в координатной форме имеет вид 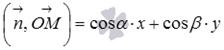 . Следовательно,
. Следовательно,  или
или  . На этом вывод нормального уравнения прямой закончен.
. На этом вывод нормального уравнения прямой закончен. , в котором числа A и B таковы, что длина вектора
, в котором числа A и B таковы, что длина вектора  равна единице, а число C неотрицательно.
равна единице, а число C неотрицательно.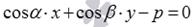 задает в прямоугольной системе координат Oxy на плоскости прямую с нормальным вектором единичной длины
задает в прямоугольной системе координат Oxy на плоскости прямую с нормальным вектором единичной длины  расположенную на расстоянии p единиц от начала координат в положительном направлении вектора
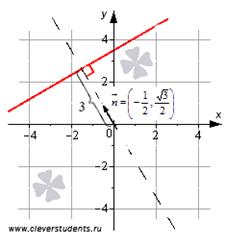
расположенную на расстоянии p единиц от начала координат в положительном направлении вектора  . Оно в прямоугольной системе координат Oxy на плоскости задает прямую линию, нормальный вектор которой имеет координаты
. Оно в прямоугольной системе координат Oxy на плоскости задает прямую линию, нормальный вектор которой имеет координаты  , и эта прямая удаленна от начала координат на 3 единицы в направлении, совпадающем с направлением нормального вектора
, и эта прямая удаленна от начала координат на 3 единицы в направлении, совпадающем с направлением нормального вектора  .
.