Способ нахождения расстояния от заданной точки до заданной прямой на плоскости.
Если мы определим координаты Осталось разобраться с нахождением координат точки H1. Мы знаем, что прямой линии в прямоугольной системе координат Oxy соответствует некоторое уравнение прямой на плоскости. Будем считать, что способ задания прямой a в условии задачи позволяет написать общее уравнение прямой a или уравнение прямой с угловым коэффициентом. После этого мы можем составить уравнение прямой, проходящей через заданную точку HYPERLINK "http://www.cleverstudents.ru/line_passes_through_point_perpendicular_to_line.html"MHYPERLINK "http://www.cleverstudents.ru/line_passes_through_point_perpendicular_to_line.html"1 HYPERLINK "http://www.cleverstudents.ru/line_passes_through_point_perpendicular_to_line.html" перпендикулярно заданной прямой a. Обозначим эту прямую буквой b. Тогда точка H1 – это точка пересечения прямых a и b, следовательно, координаты точки H1 можно определить, обратившись к материалу статьи координаты точки пересечения двух прямых. Итак, мы получили алгоритм для нахождения расстояния от заданной точки • находим общее уравнение прямой a вида • получаем общее уравнение прямой b вида • определяем координаты • вычисляем требуемое расстояние от точки M1 до прямой a по формуле
21.Различные уравнения плоскости (общее, уравнение плоскости проходящей через 3 точки уравнение плоскости в отрезках). Плоскость - есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.
|

 точки H1, то искомое расстояние
точки H1, то искомое расстояние  мы сможем вычислить, используя формулу для нахождения расстояния от точки M1 до точки H1 по их координатам:
мы сможем вычислить, используя формулу для нахождения расстояния от точки M1 до точки H1 по их координатам:  .
. до заданной прямой a:
до заданной прямой a: или уравнение прямой a с угловым коэффициентом
или уравнение прямой a с угловым коэффициентом  ;
; или уравнение прямой b с угловым коэффициентом вида
или уравнение прямой b с угловым коэффициентом вида  , учитывая, что прямая b проходит через заданную точку M1 и перпендикулярна заданной прямой a;
, учитывая, что прямая b проходит через заданную точку M1 и перпендикулярна заданной прямой a; или
или 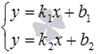 ;
;


