Угол между прямыми. Угол между прямой и плоскостьюОпределение. Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным. Угол между прямыми в пространстве равен углу между их направляющими векторами
Пример. Найти угол между прямыми
Решение. По условию
Условия параллельности и перпендикулярности прямых Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:
Пример. Найти уравнения прямой проходящей через точку Решение. Поскольку искомая прямая параллельна данной прямой, то в качестве направляющего вектора искомой прямой можно взять направляющий вектор данной прямой.
По условию
|
. Поэтому, если две прямые заданы каноническими уравнениями вида 
и 
то косинус угла между ними можно найти по формуле:
).
и 
.
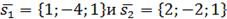, тогда
отсюда
, 
, 
.
– условие параллельности прямых.
– условие перпендикулярности прямых.
параллельно прямой 
.
, 
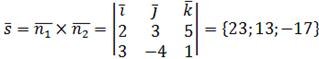– отсюда уравнение искомой прямой имеет вид: 
.
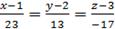