Директрисы эллипса
Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии а⁄ ε от него, называются директрисами эллипса (здесь, а — большая полуось, ε — эксцентриситет эллипса). Так как для эллипса ε < 1, то a ⁄ ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая — общее свойство, присущее эллипсу. Теорема. Если r1 — фокальное расстояние произвольной точки М эллипса до какого-нибудь фокуса, d — расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r1 ⁄d есть постоянная величина, равная эксцентриситету эллипса. Д о к а з а т е л ь с т в о. Предположим для определенности, что речь идет о правом фокусе F1 и правой директрисе. Пусть М (х; у) — произвольная точка эллипса. Расстояние от точки М до правой директрисы выражается равенством
Кроме того, r2 = a - ε·x Составляя отношение, получим
Аналогично доказывается для левого фокуса эллипса.
29. Определение гиперболы и вывод канонического уравнения. Гипербола – это геометрическое место точек для каждой из которых разность расстояний до двух заданных точек, называемых фокусами есть постоянная величина =2а и требуется что-бы эта величина была меньше, чем расстояние между фокусами. Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1 – MF2|=2a или MF1 – MF2 =±2a,
30.Определение параболы и вывод канонического уравнения. Параболой называется множеством всех таких точек плоскости, для которых расстояние до фиксированной точки F равно расстоянию до фиксированной прямой. Фиксированную точку мы будем называть фокусом, фиксированную прямую — директрисой параболы.
r = d является необходимым и достаточным условием расположения точки М на данной параболе. Так как Преобразуя формулу получим: Свойства параболы: 1°. Парабола имеет одну ось симметрии (ось Ох). Эта ось называется ось параболы. 2°. Поскольку
31.Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов отличен от нуля. Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической _квадратичнойHYPERLINK "форма%22квадратичной%20формы" HYPERLINK "форма%22квадратичной%20формы"формы, соответствующей уравнению кривой
Так, например, невырожденная кривая оказывается вещественным эллипсом, _мнимымHYPERLINK "эллипс%22мнимым%20эллипсом" HYPERLINK "эллипс%22мнимым%20эллипсом"эллипсом, гиперболой или параболой в зависимости от того, будет ли положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
или
Корни этого уравнения являются ___собственнымиHYPERLINK "пространства%22собственными%20значениями" HYPERLINK "пространства%22собственными%20значениями"значениями вещественной симметричной матрицы
и, как следствие этого, всегда вещественны.
|



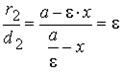



 Для вывода канонического уравнения параболы выберем начало О декартовой системы координат в середине отрезка FD, представляющего собой перпендикуляр, опущенный из фокуса F на директрису, а оси Ох и Оу направим так, как указано на рис. Пусть длина отрезка FD равна р. Тогда в выбранной системе координат точка F имеет координаты (р/2,0). Пусть М — точка плоскости с координатами (x,y). Обозначим через r расстояние от М до F, а через d – расстояние от М до директрисы. Согласно определению параболы равенство:
Для вывода канонического уравнения параболы выберем начало О декартовой системы координат в середине отрезка FD, представляющего собой перпендикуляр, опущенный из фокуса F на директрису, а оси Ох и Оу направим так, как указано на рис. Пусть длина отрезка FD равна р. Тогда в выбранной системе координат точка F имеет координаты (р/2,0). Пусть М — точка плоскости с координатами (x,y). Обозначим через r расстояние от М до F, а через d – расстояние от М до директрисы. Согласно определению параболы равенство: то
то 
 каноническое уравнение параболы
каноническое уравнение параболы ,то парабола целиком содержится в полуплоскости (х ≥ 0), граница которой перпендикулярна оси параболы.
,то парабола целиком содержится в полуплоскости (х ≥ 0), граница которой перпендикулярна оси параболы.



