Расстояние от точки до прямой в пространстве (вывод формулы). Расстояние между параллельными прямыми в пространстве.
Вывод формулы Если задано уравнение прямой l то несложно найти s(p) = {m; n; p} - направляющий вектор прямой и M1(x1, y1, z1) - координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах S = |M0M1×S(p)|. С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне S = |s|d. В нашем случае высота будет равна расстоянию от точки до плоскости d, а сторона параллелограмма равна модулю направляющего вектора s. Приравняв площади несложно получить формулу расстояния от точки до прямой. Расстояние между параллельными прямыми в пространстве Можно найти расстояние между прямыми в пространстве как расстояние между плоскостями. Расстояние между двумя параллельными плоскостями — равно длине перпендикуляра, опущенного из точки одной плоскости на другую плоскость. Если заданы уравнения параллельных плоскостей Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 =0, то расстояние между плоскостями можно найти, используя следующую формулу
28.Определение эллипса и вывод канонического уравнения.
|
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если s(p) = {m; n; p} - направляющий вектор прямой l, M1(x1, y1, z1) - точка лежащей на прямой, тогда расстояние от точки M0(x0, y0, z0) до прямой l можно найти, используя формулу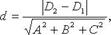
а если уравнениями 
и 
то 
