Канонические уравнения поверхностей второго порядка
Поверхность второго порядка задается в декартовых координатах уравнением второй степени Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+2Gx+2Hy+2Kz+L=0. За счет выбора специальной системы координат это уравнение преобразуется к простейшему (каноническому) виду. Цилиндрические поверхности:
г) – эллипсоид;
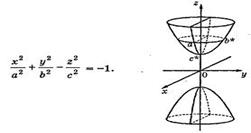
д) – двуполостный гиперболоид;
е) – однополостный гиперболоид;
ж) – эллиптический параболоид.
35.Цилиндрической называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению (рис. 4.11). Уравнение цилиндрической поверхности, образующие которой параллельны оси Особенность уравнения (4.48) состоит в том, что оно не содержит переменной Цилиндрическая поверхность с образующей, параллельной оси Поверхность с образующей, параллельной оси
Вокруг оси
Поверхность, образованная вращением линии Имеет уравнение Поверхность, образованная вращением линии Ох, определяется уравнением . Поверхностью вращения второго порядка называется поверхность, полученная вращением линии второго порядка вокруг ее оси. Эллипсоидом вращения называется поверхность, полученная вращением эллипса вокруг одной из его осей. Уравнение эллипсоида вращения, полученного вращением эллипса
Однополосным гиперболоидом вращения называется поверхность, полученная вращением гиперболы вокруг ее мнимой оси. Однополосный гиперболоид вращения, полученный вращением гиперболы
Двуполостным гиперболоидом вращения называется поверхность, полученная вращением гиперболы вокруг ее действительной оси. Двуполо-стный гиперболоид, полученный вращением гиперболы
Параболоидом вращения'называется поверхность, полученная вращением параболы вокруг ее оси. Уравнение параболоида вращения, полученного вращением параболы
• Пример 4.23. Составить уравнение поверхности, полученной вращением линии. Данные уравнения определяют пару пересекающихся прямых в плоскости
В соответствии с уравнением (4.50) получаем
Последнее уравнение является уравнением конуса вращения, получающегося при вращении указанных прямых вокруг оси Эллиптический цилиндр. Уравнение
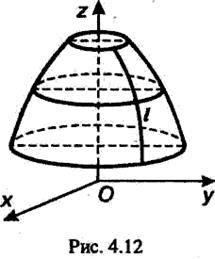
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ, направляющей является эллипсс полуосями a и b (рис. 1).
В частности, уравнение x 2 + y 2 = R 2 в трехмерном пространстве определяет круглый цилиндр. Гиперболический цилиндр. Уравнение
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ, направляющей является гиперболас полуосями a и b (рис. 2).
Параболический цилиндр. Уравнение
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ, направляющей является парабола (рис. 3).
36. Ко́мпле́ксные чи́сла (0110008070 устар. 090080005108100 Мнимые числа ), — расширение 090005000030501100 поля 00510511020500005108100 вещественных чисел, обычно обозначается Комплексные числа образуют 0003050110008105100807000001100500005алгебраически замкнутое 090005000030501100поле — это означает, что 090003010050многочлен степени Поле комплексных чисел можно понимать как 000011081050080500018расширение поля вещественных чисел, в котором многочлен
|
Имеет вид
Есяи уравнение 
Определяет некоторую поверхность, то ею является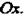
Если уравнение 
Определяет некоторую поверхность, то ею является цилиндрическая
Поверхность, образованная вращением линии 
(4.49)
(рис. 4.12), определяется уравнением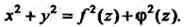
(4.50)
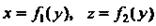Вокруг оси 
,
Вокруг оси
Вокруг оси 
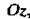, имеет вид 
Вокруг оси 
Имеет уравнение
,
Вокруг оси 
, определяется уравнением
Вокруг оси 
Имеет вид
Вокруг оси 
проходящих через начало координат (являющихся пересечением плоскостей 
С плоскостью 
). Приведем эти уравнения к виду (4.49):
– эллиптический цилиндр;
б) 
– гиперболический цилиндр;
в) 
– параболический цилиндр;
г) 
– сфера;
д) 
– эллипсоид;
е) 
– двуполостный гиперболоид;
ж) 
– однополостный гиперболоид;
з)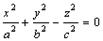 
– конус;
и) 
– эллиптический параболоид.
. Любое комплексное число может быть представлено как формальная сумма 
, где 
и 
— вещественные числа, 
— 0900800018050408008100мнимая единица.
с комплексными коэффициентами имеет ровно 
имеет корень. Следующие две элементарные 0900405018108110501800010800модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к 0070001108070000105000108000изоморфным расширениям поля вещественных чисел 
, как и любые другие конструкции 0900051000700060500818поля разложения многочлена 
