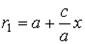Исследование формы эллипса

Так как

 

то эллипс лежит внутри прямоугольника со сторонами х = ± а, у = ± b.

 

Эллипс является симметричным относительно начала координат и относительно осей координат. Это следует из-за того, что в уравнении эллипса переменные x и y входят квадратами x2, y2. Если уравнению эллипса удовлетворяет точка с координатами x и y, то уравнению эллипса будут удовлетворять точки с координатами (−x, − y), (− x, y), (x, − y).

Фокусы эллипса лежат на его большой оси эллипса.

 

Соотношения для фокальных расстояний эллипса

Убедимся в том, что если координаты точки удовлетворяют каноническому уравнению эллипса, то сумма расстояний этой точки до двух точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Для этого, очевидно, достаточно показать, что величины r1 и r2 для любой точки, координаты которой удовлетворяют уравнению эллипса, удовлетворяют соотношению r1 + r2= 2·a.

 

Найдём из уравнения эллипса

 

и подставим это выражение в соотношение

 

Получим

После преобразования получим соотношение для фокального радиуса

 

Так как по определению с < a и | х | < a, то выражение в скобках под знаком корня положительно, поэтому

Аналогично найдём

 

Складывая фокальные расстояния, получим r1 + r2 = 2·a

Что и требовалось доказать. Таким образом, эллипс — линия второго порядка.

Замечание. Если а = b, то уравнение эллипса принимает вид x2 + y2= a2. Это уравнение окружности радиуса а. Таким образом, окружность — частный случай эллипса. Заметим, что эллипс можно получить из окружности радиуса а, если сжать ее в а ⁄ b раз вдоль оси Оу.

Оси симметрии эллипса называются его осями, а центр симметрии (точка пересечения осей) — центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами. Вершины ограничивают на осях отрезки, равные 2·а и 2·b. Если а ≥ b, величины а и b называются соответственно большой и малой полуосями эллипса.