Стандартная модель
Комплексное число • • Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные 0010800001080000205105110205001811081050операции с вещественными числами. Исключением являются только свойства, связанные с 09100105008050011804000отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно. Действия над комплексными числами • Сравнение
• Сложение
• Вычитание
• Умножение
• Деление
Геометрическая модель
Геометрическое представление комплексного числа Рассмотрим плоскость с 09118001030018000181081105000000104080001%прямоугольной системой координат. Каждому комплексному числу Часто бывает удобно рассматривать на комплексной плоскости также 0900181000181081105000000104080001%полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол000004081102050101%радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже. В этом наглядном представлении сумма комплексных чисел соответствует 005010103050005110818векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в 00010000810510080500005010000818теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «000008110400амплитуда» и «0400070000005010000809фаза». Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Часто этот метод даёт наиболее простое доказательство. Связанные определения Пусть • Если • Если
|

 можно определить как упорядоченную пару 00510511020500005108100вещественных чисел
можно определить как упорядоченную пару 00510511020500005108100вещественных чисел  . Введём операции сложения и умножения таких пар следующим образом:
. Введём операции сложения и умножения таких пар следующим образом:

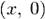 , причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой
, причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой  единица —
единица — 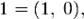 а 0900800018050408008100мнимая единица —
а 0900800018050408008100мнимая единица —  На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен
На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен 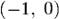 , то есть
, то есть 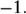
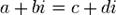 означает, что
означает, что  и
и  (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
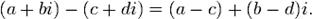




 сопоставим точку плоскости с координатами
сопоставим точку плоскости с координатами  (а также 000004081102050101%радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется 0900000501000180001001118комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.
(а также 000004081102050101%радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется 0900000501000180001001118комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями. — комплексное число, где
— комплексное число, где  и
и  — 00510511020500005108100вещественные числа. Числа
— 00510511020500005108100вещественные числа. Числа  или
или  и
и  или
или  называются соответственно вещественной и мнимой (аналогично 0003008091008091807180англ. real, imaginary) частями
называются соответственно вещественной и мнимой (аналогично 0003008091008091807180англ. real, imaginary) частями  , то
, то  , то
, то 


