Алгебраическая форма
Запись комплексного числа Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что
Тригонометрическая и показательная формы Если вещественную
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через 040101000009005100формулу Эйлера:
где Отсюда вытекают следующие широко используемые равенства:
37. 38. Понятие "степень комплексного числа" в силу определения операции умножения (23) вводится аналогично обычному алгебраическому, т. е. под степенью числа
и тогда на основе этого определения можно расширить свойства комплексной экспоненты, рассмотренные в 3-3.%22примере%20HYPERLINK%20%22.html%22примере%201-3.%221HYPERLINK%20%22.html%22примере%201-3.%22-HYPERLINK%20%22.html%22примере%201-3.%223HYPERLINK%20%22.html%22примере%201-3.%22."примере HYPERLINK "3.%22примере%20HYPERLINK%20%22.html%22примере%201-3.%221HYPERLINK%20%22.html%22примере%201-3.%22-HYPERLINK%20%22.html%22примере%201-3.%223HYPERLINK%20%22.html%22примере%201-3.%22."1HYPERLINK "3.%22примере%20HYPERLINK%20%22.html%22примере%201-3.%221HYPERLINK%20%22.html%22примере%201-3.%22-HYPERLINK%20%22.html%22примере%201-3.%223HYPERLINK%20%22.html%22примере%201-3.%22."-HYPERLINK "3.%22примере%20HYPERLINK%20%22.html%22примере%201-3.%221HYPERLINK%20%22.html%22примере%201-3.%22-HYPERLINK%20%22.html%22примере%201-3.%223HYPERLINK%20%22.html%22примере%201-3.%22."3HYPERLINK "3.%22примере%20HYPERLINK%20%22.html%22примере%201-3.%221HYPERLINK%20%22.html%22примере%201-3.%22-HYPERLINK%20%22.html%22примере%201-3.%223HYPERLINK%20%22.html%22примере%201-3.%22.". Пример 1-4. Показать, что Решение. Из (413) и с помощью свойства 2 из 3-3%22Примера%20HYPERLINK%20%22.html%22Примера%201-3%221HYPERLINK%20%22.html%22Примера%201-3%22-HYPERLINK%20%22.html%22Примера%201-3%223"Примера HYPERLINK "3%22Примера%20HYPERLINK%20%22.html%22Примера%201-3%221HYPERLINK%20%22.html%22Примера%201-3%22-HYPERLINK%20%22.html%22Примера%201-3%223"1HYPERLINK "3%22Примера%20HYPERLINK%20%22.html%22Примера%201-3%221HYPERLINK%20%22.html%22Примера%201-3%22-HYPERLINK%20%22.html%22Примера%201-3%223"-HYPERLINK "3%22Примера%20HYPERLINK%20%22.html%22Примера%201-3%221HYPERLINK%20%22.html%22Примера%201-3%22-HYPERLINK%20%22.html%22Примера%201-3%223"3 получим
Переход к комплексным числам в показательной форме оказывается очень удобным приемом в случае преобразований тригонометрических функций. Пример 1-5. Доказать, что Решение. Из 3формулы Эйлера
Учитывая свойства функции
Раскрывая степень с помощью формулы бинома Ньютона, имеем
где
где символ
Отметим, что формула (414) для полиномов Чебышева может быть переписана как формула Муавра. Действительно, обозначая
Корнем степени
Пример 1-6. Вычислить все значения следующих корней: 1.
|

 в виде
в виде  ,
, 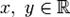 , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.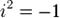 ):
):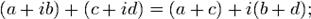
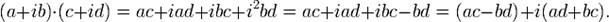
 и мнимую
и мнимую  части комплексного числа выразить через модуль
части комплексного числа выразить через модуль 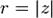 и аргумент
и аргумент 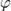 (
(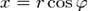 ,
, 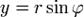 ), то всякое комплексное число
), то всякое комплексное число 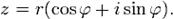
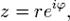
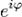 — расширение 001000050100экспоненты для случая комплексного показателя степени.
— расширение 001000050100экспоненты для случая комплексного показателя степени.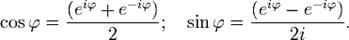
 понимается
понимается 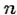 -кратное повторение умножения:
-кратное повторение умножения: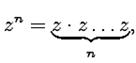
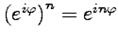 .
.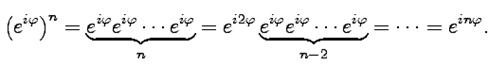
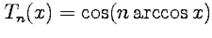 является алгебраическим многочленом степени
является алгебраическим многочленом степени 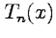 c
c 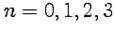 .
.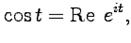 и, следовательно:
и, следовательно: 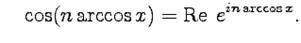
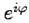 и применяя формулу Эйлера еще раз, получим
и применяя формулу Эйлера еще раз, получим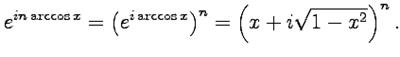
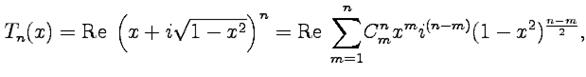
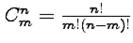 - биномиальные коэффициенты. Из последнего выражения видно, что слагаемые с четными
- биномиальные коэффициенты. Из последнего выражения видно, что слагаемые с четными 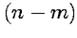 будут действительными величинами, которые являются целыми степенями
будут действительными величинами, которые являются целыми степенями 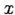 , максимальная из которых равна
, максимальная из которых равна 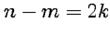 , можно получить действительное выражение для
, можно получить действительное выражение для 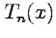 в виде
в виде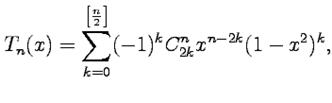
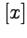 означает целую часть
означает целую часть 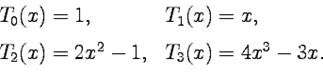
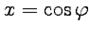 , получим
, получим 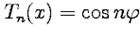 , и тогда из (414):
, и тогда из (414):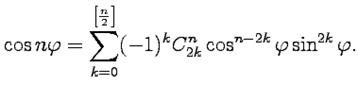
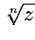 , такое, что его
, такое, что его 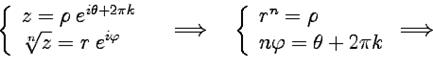
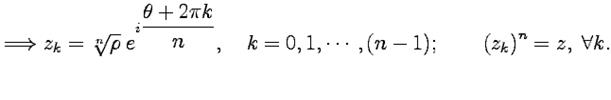
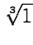 2.
2. 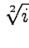 3.
3. 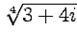 .
.


