Геометрический смысл смешанного произведенияГеометрический смысл смешанного произведения: если 4_4.php"тройка векторов Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах
Свойства смешанного произведения: 1° 2° 3° Три 4_0.php"вектора компланарны тогда и только тогда, когда 4° Тройка векторов является правой тогда и только тогда, когда 5° 6° 7° 8° 9° 10° Тождество Якоби: Если векторы Объем параллелепипеда определяется по формуле
Пусть координаты векторов
Рассмотрим выражение В этих обозначениях векторное произведение можно записать в виде Можно показать, что аналогично плоскому случаю знак
|
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 
. В случае левой тройки 
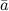. Если 
, 
и 
компланарны, то их смешанное произведение равно нулю.
. Если же 
, то векторы 
, 
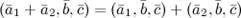
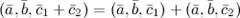
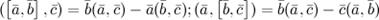
и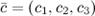 
заданы своими координатами, то их смешанное произведение вычисляется по формуле
, где 
— угол между векторами 
и 
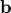, а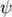 
— угол между вектором 
и перпендикуляром к плоскости, в которой лежат 
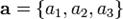
. В ортонормированном базисе
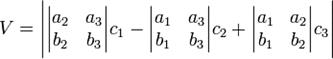
. Это выражение называют определителем трехмерной матрицы и обозначают 
.
.
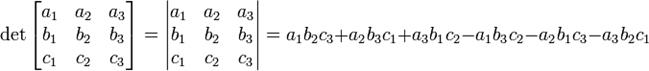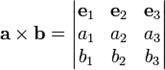совпадает с ориентацией тройки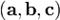 
.
