Нахождение теоретической формы связи в корреляционном анализе. Критерий адекватности математических функций в корреляционном анализе.
При исследовании корреляционных связей между качественными признаками, представленными в виде альтернативных показателей, используют коэффициент ассоциации Юла (Ка) и коэффициент контингенции Пирсона (Кк). Коэффициент ассоциации: Ка = (а·d – b·c) ÷ (а·d + b·c). В тех случаях, когда один из показателей отсутствует, величина коэффициента ассоциации будет равна 1, что дает неправильную оценку степени тесноты связи между признаками. В этом случае используют коэффициент контингенции:
Кк изменяется от –1 до +1, Кк < Ка всегда. Чем ближе коэффициент контингенции к единице, тем сильнее связь между факторным и результативным признаками.
ДА НЕТ ДА а в НЕТ с d, Для оценки значимости индекса корреляции применяется F-критерий Фишера.
Где m – число параметров корреляционного уравнения. Величина FR – сравнивается с критическим значением FK. Если FR> FK, то величина R признается существенной и синтезированная математическая модель может быть пригодной для практического использования. в качестве критерия адекватности синтезируемых моделей использ-ся показатели минимальности сркдней ошибки аппроксимации.
|
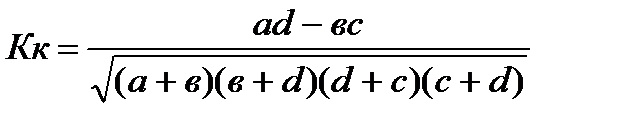
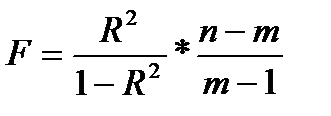
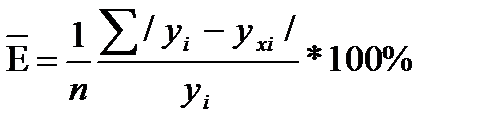, где уi-yxi линейное отклонение абсолютных велечин эмпирических и выравненых точек регрессии.
