Расчет среднего уровня в рядах динамики.
Средний уровень ряда для интервального ряда динамики определяется: где ∑ уi - это сумма уровней ряда; n – число уровней. Средний уровень моментного ряда динамики с равными интервалами:
где n – число уровней ряда динамики. Средний уровень моментного ряда с неравными интервалами
где Показатели и анализа рядов динамики. Абсолютный прирост – разность уровней ряда. Базисный абсолютный прирост: ∆уб = уi – уо, Цепно,й абсолютный прирост: ∆уn = уi – уi –1 , Темпы роста – отношение уровней ряда одного периода к другому, выражаются в процентах и коэффициентах. Базисные темпы роста: Тр б = (уi /уо) ·100% Цепные темпы роста: Тр ц = (уi / уi –1) · 100% Темпы прироста характеризуют абсолютный прирост в относительных величинах, выражаются в процентах и коэффициентах. Базисный темп прироста: ∆Тпр б = ((уi – уо) ÷ уо) · 100% Цепной темп прироста: ∆Тпр ц = ((уi – уi –1) ÷ уi –1) · 100%. Темп прироста можно получить из темпа роста: ∆Тпр б = Тр б – 100%; ∆Тпр ц = Тр ц – 100%. Средний абсолютный прирост – обобщенная характеристика индивидуальных приростов ряда динамики. ∆уц = ∑(∆уц) ÷ n. Средний темп роста: Тр =ⁿ√ Тр 1 · Тр 2 · … · Тр n; Тр =ª√ yn÷уо, где Тр 1, Тр 2, …, Тр n – индивидуальные темпы роста; n – число индивидуальных темпов роста; а – число уровней ряда минус 1. Средний темп прироста: ∆Тп (%) = Тр (%) – 100%, ∆Тп = Тр – 1. Абсолютное значение 1 % прироста А =
|
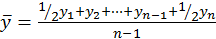
– время интервала между признаками.
=0,01 уi-1
