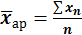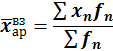Средние величины, их сущность и значение. Основные правила применения средних в статистике. Правило мажорантности средних.
Средние величины – это обобщающие показатели, в которых находят выражение действия общих условий, закономерность изучаемого явления. Признак по кот нах-ся средняя наз осредняемым и величина осредненного признака у каждой ед-цы сов-ти наз индивидуализ-ым ее значением или вариантой Повторяемость вариант наз частота.
Где х-вариант признака n- число вариантов m- показатель степени средней если m=1, то получаем Средняя арифметическая: m=2 получаем Средняя квадратическая: m=-1 Средняя гармоническая: m=0 Средняя геометрическая:
Выше были приведены простые средние. Их используют только тогда, когда у каждой варианты частота равна единице или частоты всех вариант равны. Когда в ряду распределения одно и то же значение признака встречается несколько раз, рассчитывают средние взвешенные: - средняя арифметическая,
где f – частота (весы), повторяемость индивидуальных значений признака. Взвешивание – это умножение каждой варианты на соответствующую частоту.
Средняя арифметическая используется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение. - средняя гармоническая,
|
;
;
;
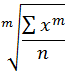
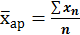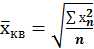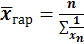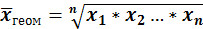
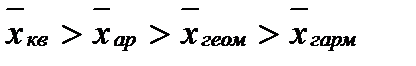- правило мажорности средних.
