Распространение выборочных характеристик на генеральную совокупность.
Конечной целью выборочного наблюдения является характеристика генеральной совокупности. При малых объемах выборки эмпирические оценки параметров ( Доверительным интервалом какого-либо параметра генеральной совокупности называется случайная область значений этого параметра, которая с вероятностью близкой к 1 (надежностью) содержит истинное значение этого параметра. Предельная ошибка выборки (∆ = tµ, где ∆– предельная ошибка выборки; – средняя ошибка выборки; t – коэффициент доверия, определяемый по таблице интегральной функции Лапласа при заданной вероятности.) позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы. Нижняя граница доверительного интервала получена путем вычитания предельной ошибки из выборочного среднего (доли), а верхняя — путем ее добавления. Доверительный интервал для средней использует предельную ошибку выборки и для заданного уровня достоверности определяется по формуле: Истинное значение средней: Где Существуют два основных метода распространения выборочного наблюдения на генеральную совокупность: прямой пересчет и способ коэффициентов. Сущность прямого пересчета заключается в умножении выборочного среднего значения на объем генеральной совокупности. Способ коэффициентов целесообразно использовать в случае, когда выборочное наблюдение проводится с целью уточнения данных сплошного наблюдения. При этом используют формулу: Y1=Y0
|

 ) могут существенно отклоняться от их истинных значений (µ и р). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров (
) могут существенно отклоняться от их истинных значений (µ и р). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров ( .
. - генеральная средняя величина, Δх — предельная ошибка выборочной средней. Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от
- генеральная средняя величина, Δх — предельная ошибка выборочной средней. Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от 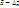 до
до 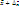 . Истинное значение доли: w − Δw ≤ ρ ≤ w + Δw.
. Истинное значение доли: w − Δw ≤ ρ ≤ w + Δw. , где все переменные — это численность совокупности: Y1— с поправкой на недоучет, Y0- без этой поправки, y0— в контрольных точках; y1 — в тех же точках по данным контрольных мероприятий.
, где все переменные — это численность совокупности: Y1— с поправкой на недоучет, Y0- без этой поправки, y0— в контрольных точках; y1 — в тех же точках по данным контрольных мероприятий.


