Показатели вариации и методы их расчета.
Для целей аналитической и сравнительной характеристики различных рядов распределения принимается система обобщающих пок-лей вариационного ряда. Мода и медиана относятся к показателям центра распределения. Группы показателей вариации: 1)Показатели центра распределения (ср вел-на и структурные средние). 2)Показатели степени вариации. 3)Показатели формы распределения. Показатели размера и интенсивности вариации: Размах вариации: Среднее линейное отклонение ( d) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения: Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины: Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Чаще всего они выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному). Относительные показатели вариации:– коэффициент осцилляции: V =R: Показатели формы распределения. Степень асимметрии может быть определена с помощью коэффициента асимметрии (Аs):
где Симметричным наз. распределение, в кот. частоты 2-ух любых вариантов, равностоящих в обе стороны от центра распределения равны м/у собой. При симметричном (нормальном) распределении имеется правосторонняя асимметрия. Если As < 0-левосторонняя асимметрия. Коэффициент асимметрии может изменяться от –3 до +3. Для симметричных распределений может быть также рассчитан показатель эксцесса, характеризующий крутизну распределения:
|

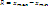 , где xmax и xmin – максим и миним значение варьирующих признаков.
, где xmax и xmin – максим и миним значение варьирующих признаков. – невзвешенное среднее линейное отклонение;
– невзвешенное среднее линейное отклонение;  - взвешенное среднее линейное отклонение, где xi – i-й вариант осредняемого признака, fi – вес i-го варианта.
- взвешенное среднее линейное отклонение, где xi – i-й вариант осредняемого признака, fi – вес i-го варианта. - невзвешенная;
- невзвешенная;  - взвешенная. Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии; величина именованная, имеет размерность осредняемого признака.
- взвешенная. Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии; величина именованная, имеет размерность осредняемого признака. ⋅100%, – линейный коэффициент вариации: V =d:
⋅100%, – линейный коэффициент вариации: V =d: 
 – средняя арифметическая ряда распределения; Mo – мода;σ – среднее квадратическое отклонение.
– средняя арифметическая ряда распределения; Mo – мода;σ – среднее квадратическое отклонение. где µ4– центральный момент четвертого порядка.При симметричном распределении Ex = 0; Ex > 0, распределение островершинное; если Ex < 0 – плосковершинное.
где µ4– центральный момент четвертого порядка.При симметричном распределении Ex = 0; Ex > 0, распределение островершинное; если Ex < 0 – плосковершинное.


