Вопрос 24. Правило сложения дисперсий и его использование в анализе взаимосвязи
Показатели вариации могут быть использованы не только в анализе изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями. Для сгруппированной, т. е. разделенной на i групп, статистической совокупности возможно вычисление трех видов дисперсий общей, внутригрупповых и межгрупповой. Общая дисперсия (
Где Для оценки колеблемости признака внутри каждой i-ой группе вычисляют внутригрупповые дисперсии (
Межгрупповая дисперсия (
Между всеми указанными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий- общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии: σ2 = σ¯xi2+ δ2 Логика этого правила такова: общая вариация признака в совокупности складывается из вариаций признака внутри отдельных групп и вариаций между группами. Правило сложения дисперсий широко применяется при исчислении показателей тесноты связей, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев. На основании правила сложения дисперсий можно определить показатель тесноты связи между факторным и результативным признаками. Он наз-ся эмпирическим корреляционным отношением и рассчитывается по формуле:
27/2
Пределы доли признака в генеральной совокупности (р) рассчитываются следующим образом: w − Δw ≤ ρ ≤ w + Δw. Ошибки и пределы генеральных характеристик при других способах формирования выборочной совокупности определяются на основе соответствующих формул, отражающих особенности этих видов выборки. Например, в случае типической выборки показателем вариации является средняя из внутригрупповых дисперсий, при серийной выборке – межгрупповая (межсерийная) дисперсия и т.д. Кроме того, в последнем случае вместо объема выборочной совокупности n используется показатель
|

 ) характеризует колеблемость признака признака во всей изучаемой сов-ти и рассчитывается по не сгруппированным данным по формуле
) характеризует колеблемость признака признака во всей изучаемой сов-ти и рассчитывается по не сгруппированным данным по формуле
 среднее значение признака в совокупности;
среднее значение признака в совокупности;  -число единиц в i-ой группе.
-число единиц в i-ой группе.
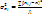 ,Где
,Где  -среднее значение признака в i-ой группе. Обобщённую характеристику внутригрупповой колеблемости вокруг групповых средних дает средняя величина из внутригрупповых дисперсий:
-среднее значение признака в i-ой группе. Обобщённую характеристику внутригрупповой колеблемости вокруг групповых средних дает средняя величина из внутригрупповых дисперсий:
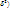 показывает вариацию групповых средних вокруг средней величины признака в совокупности:
показывает вариацию групповых средних вокруг средней величины признака в совокупности:





