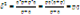Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой взвешенной и невзвешенной:  - невзвешенная;
- невзвешенная;  - взвешенная. Рассчитать дисперсию можно также по преобразованной формуле:
- взвешенная. Рассчитать дисперсию можно также по преобразованной формуле:  , где
, где  –средний квадрат значений признака в совокупности:
–средний квадрат значений признака в совокупности: 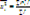 ,
,  -квадрат среднего значения признака в совокупности. При расчете дисперсии по этой формуле исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от его средней величины, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений. Св-ва дисперсии: 1. б2(а) = 0 – дисперсия постоянной величины равна нулю. 2. б2(а+х) = б2(х) – дисперсия не меняется, если все варианты увеличить/уменишить на одно и то же число. 3. б2(ах) = а2 * б2(х) –если все варианты умножить на число а, дисперсия увеличится в а2 раз. 4 Если исчислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (х), то он всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической:
-квадрат среднего значения признака в совокупности. При расчете дисперсии по этой формуле исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от его средней величины, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений. Св-ва дисперсии: 1. б2(а) = 0 – дисперсия постоянной величины равна нулю. 2. б2(а+х) = б2(х) – дисперсия не меняется, если все варианты увеличить/уменишить на одно и то же число. 3. б2(ах) = а2 * б2(х) –если все варианты умножить на число а, дисперсия увеличится в а2 раз. 4 Если исчислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (х), то он всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической:  . Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней и этой условно взятой величины, т.е. на (
. Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней и этой условно взятой величины, т.е. на ( - A)2:
- A)2: 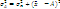 , или
, или
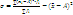 . Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности.
. Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности.
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:  . Подставляя в данную формулу дисперсии q =1- р, получаем:
. Подставляя в данную формулу дисперсии q =1- р, получаем: 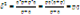

 - невзвешенная;
- невзвешенная;  - взвешенная. Рассчитать дисперсию можно также по преобразованной формуле:
- взвешенная. Рассчитать дисперсию можно также по преобразованной формуле:  , где
, где  –средний квадрат значений признака в совокупности:
–средний квадрат значений признака в совокупности: 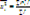 ,
,  -квадрат среднего значения признака в совокупности. При расчете дисперсии по этой формуле исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от его средней величины, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений. Св-ва дисперсии: 1. б2(а) = 0 – дисперсия постоянной величины равна нулю. 2. б2(а+х) = б2(х) – дисперсия не меняется, если все варианты увеличить/уменишить на одно и то же число. 3. б2(ах) = а2 * б2(х) –если все варианты умножить на число а, дисперсия увеличится в а2 раз. 4 Если исчислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (х), то он всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической:
-квадрат среднего значения признака в совокупности. При расчете дисперсии по этой формуле исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от его средней величины, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений. Св-ва дисперсии: 1. б2(а) = 0 – дисперсия постоянной величины равна нулю. 2. б2(а+х) = б2(х) – дисперсия не меняется, если все варианты увеличить/уменишить на одно и то же число. 3. б2(ах) = а2 * б2(х) –если все варианты умножить на число а, дисперсия увеличится в а2 раз. 4 Если исчислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (х), то он всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической:  . Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней и этой условно взятой величины, т.е. на (
. Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней и этой условно взятой величины, т.е. на ( - A)2:
- A)2: 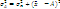 , или
, или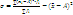 . Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности.
. Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности. . Подставляя в данную формулу дисперсии q =1- р, получаем:
. Подставляя в данную формулу дисперсии q =1- р, получаем: