Относительные показатели вариации.
В отличие от абсолютных показателей вариации, назначение относительных показателей – оценка вариации признака в % (либо в коэффициентах). Они рассчитываются как отношение абсолютных показателей вариации к средней арифметической величине признака. Наиболее простыми и менее распространенными относительными показателями являются: - коэффициент осцилляции: - относительное линейное отклонение или линейный коэффициент вариации: Cамым распространенным относительным показателем вариации является коэффициент вариации: По величине коэффициента вариации можно судить о степени вариации признаков совокупности. На практике коэффициент вариации находит широкое применение для сравнения вариации одного и того же признака в разных совокупностях (как в нашем примере), а также для сравнения вариации разных признаков одной и той же совокупности. Кроме этого, коэффициент вариации используется в оценке ритмичности работы предприятия. Совокупность считается достаточно однородной, если V ≤ 30 %.
29.Дисперсия, её виды и свойства. Вариация признака складывается под воздействием множества факторов, т.к. социально-экономические явления и процессы носят сложный характер. В исследованиях иногда возникает необходимость оценить не только общую вариацию признака, но и ту ее часть, которая обусловлена действием постоянных, стабильных, а не случайных факторов. В этих случаях рассчитывают три вида дисперсии: - общую; - межгрупповую; - внутригрупповую. Общая дисперсия характеризует общую вариацию признака под влиянием всех факторов (условий, причин).
Для определения влияния постоянного фактора на вариацию признака производят аналитическую группировку, в основании которой лежит данный фактор. Вариация, обусловленная фактором, положенным в основание группировки, оценивается с помощью межгрупповой дисперсии:
Для определения влияния случайных факторов рассчитывают дисперсию внутри каждой группы, т.е. внутригрупповую
а затем среднюю из внутригрупповых дисперсий
Доказано, что общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий.
Оно показывает тесноту связи между признаками (раздел 10). Возведенное в квадрат эмпирическое корреляционное отношение представляет собой коэффициент детерминации (δ^2), который характеризует долю общей колеблемости признака-результата, вызванную действием признака-фактора, положенного в основаниегруппировки. Наряду с вариацией количественного признака часто возникает необходимость измерить вариацию альтернативного признака. Если ввести обозначения: 1 – наличие интересующего исследователя признака; 0 – отсутствие интересующего исследователя признака; p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком, то среднее значение альтернативного признака будет равно:
Тогда дисперсия альтернативного признака определяется по формуле Дисперсия облает рядом математических свойств, которые значительно упрощают её вычисление. К основным из них относятся следующие: 1. Если все значения признака увеличить или уменьшить в А раз, то дисперсия соответственно увеличится или уменьшится в A2 раз. 2. Если все значения признака увеличить или уменьшить на какое- то постоянное число x0, то дисперсия от этого не изменится. 3. Если все значения частот различить или умножить на какое-то число b, то дисперсия от этого не изменится.
|


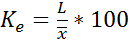

 ,
, -средняя по всей изучаемой совокупности.
-средняя по всей изучаемой совокупности.
 - средняя по отдельным группам
- средняя по отдельным группам -численность отдельных групп
-численность отдельных групп ,
,






