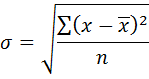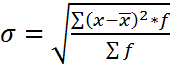Абсолютные показатели вариации.
К числу абсолютных показателей вариации относят: - размах вариации; - среднее линейное отклонение; - дисперсию; - среднее квадратическое отклонение. Размах вариации – это разность между максимальным и минимальным значениями признака
Преимущество данного показателя: простота его исчисления. Недостатки: 1) он не учитывает внутреннююколеблемость уровней ряда; 2) он часто зависит от случайности. Среднее линейное отклонение – это средняя арифметическая величина, исчисленная из абсолютных отклонений индивидуальных значений признаков от средней величины. Однако, учитывая нулевое свойство средней арифметической: сумма отклонений индивидуальных значений признака от средней равна 0. Поэтому при исчислении среднего линейного отклонения суммируются модули этих отклонений. Т.е. формулы исчисления среднего линейного отклонения имеют вид:
Преимущество среднего линейного отклонения перед размахом в том, что оно учитывает внутреннюю вариацию уровней ряда. Недостаток: необходимо абстрагирование от знака отклонения, следовательно – трудности в применении математических методов анализа вариации. Дисперсия – это средняя из квадратов отклонений индивидуальных значений признака от его средней величины. - для простого вариационного ряда
Недостаток этого показателя вариации – его размерность. Размерность дисперсии равна квадрату размерности изучаемого признака. Этот недостаток устраняется при переходе к среднему квадратическому отклонению. Среднее квадратическое отклонение определяется как квадратный корень из среднего квадрата отклонений индивидуальных значений признака от их средней величины, т.е.: - для простого вариационного ряда
- для дискретного ряда Среднеквадратическое отклонение (в иностранной литературе – стандартное отклонение) является общепринятым показателем не только в статистике, но и в технике, в биологии и др. областях знаний. Между средним линейным и средним квадратическим отклонением в распределениях, близких к нормальному, существует следующее примерное соотношение: σ ≈1.25l.
|

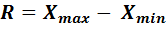
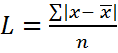 для простого вариационного ряда (для несгруппированных данных), либо
для простого вариационного ряда (для несгруппированных данных), либо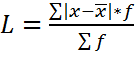 для дискретного ряда (для сгруппированных данных).
для дискретного ряда (для сгруппированных данных).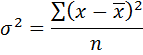
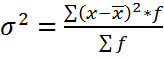 - для дискретного ряда
- для дискретного ряда