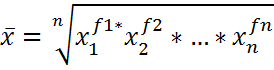Основные виды средних величин и техника их расчета по различным рядам распределения. Мажорантность средних величин.
Основанием для расчёта средних величин является определяющее свойство средней. Оно заключается в том, что сумма (а при исчислении некоторых видов средних – произведение) индивидуальных значений признака равна сумме (произведению) средних значений признака. Все средние величины делятся на два больших класса: - степенные средние; - структурные средние. Из степенных средних в экономических исследованиях наибольшее распространение получили: 1) средняя арифметическая; 2) средняя гармоническая; 3) средняя геометрическая; 4) средняя квадратическая; 5) другие виды (например, средняя хронологическая). К структурным средним относят моду и медиану. Степенные средние в зависимости от представления исходных данных могут быть: - простыми; - взвешенными. Простая средняя рассчитывается по несгруппированным данным, а взвешенная – по сгруппированным, то есть по дискретным или интервальным рядам, в которых указываются не только значения признака (x), но и частоты (повторяемости) – (f). 1. Наиболее распространённым видом средней величины является средняя арифметическая. Она может быть: - простая; - взвешенная. Простая средняя арифметическая величина исчисляется в тех случаях, когда имеется несколько различных индивидуальных величин одного и того же вида. Тогда все они суммируются, и полученная сумма делится на их число. Если обозначить эти индивидуальные значения х1,х2,х3,х4 …, а число индивидуальных значений (единиц наблюдения) – n, то средняя арифметическая простая будет равна: По сгруппированным данным рассчитывается средняя арифметическая взвешенная. Её формула: Частоты (f) в данном случае называют весами, поэтому средняя арифметическая взвешенная. Аналогичным образом, по формуле средней арифметической взвешенной, рассчитывается средняя из интервального ряда. Однако в данном случае 2. Средняя гармоническая величина применяется в тех случаях, когда известны индивидуальные значения признака x и произведения x*f, но отсутствуют частоты f. В данном случае произведение x*f обозначается W и средняя рассчитывается по формуле. Средняя в такой форме называется средней гармонической взвешенной. Средняя гармоническая взвешенная определяется по сгруппированным данным. В тех же случаях, когда произведения x*f одинаковы или равны единице, применяется средняя гармоническая простая. Область применения средней гармонической простой очень узкая: применяется в тех случаях, когда показатели связаны как x и 1. 3. Средняя геометрическая применяется в тех случаях, когда необходимо исчислить среднюю из относительных показателей: коэффициентов роста в рядах динамики. Средняя геометрическая равна корню степени n из произведений коэффициентов роста. Средняя геометрическая простая:
Такая средняя геометрическая носит название простой.
В свою очередь, средняя геометрическая взвешенная может быть определена по формуле Средняя квадратическая применяется в тех случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций (то есть когда вместо данных об индивидуальных значениях признака имеются данные об их квадратах). Например, средний диаметр труб, средняя сторона квадрата и т.д. Она также может иметь форму простой среднейквадратической:
либо форму взвешенной средней квадратической:
5. Другие виды средних величин. - средняя прогрессивная (рассчитывается при анализе выполнения норм выработки); - средняя хронологическая (рассчитывается при анализе развития явления во времени и т.д.).
|

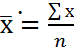

 где x′− середины или центры интервалов.
где x′− середины или центры интервалов.