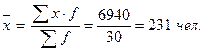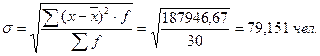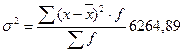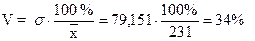Задание 1. Исследование структуры совокупности

Построим статистический ряд распределения организаций по признаку «Среднесписочная численность работников» выпуск продукции, образовав пять групп с равными интервалами.

Max численность: 450 чел.

Min численность: 50 чел.

Размер интервала: =(450-50)/5=80 чел.

Рассчитаем размеры интервалов для группировки предприятий.

 

Расчет размера интервала для группировки предприятий по признаку «Среднесписочная численность работников», чел

Расчет	Интервал
Нижняя граница	Верхняя граница	Нижняя граница	Верхняя граница
	50+80	До 130
	130+80
	210+80
	290+80
	370+80	370 и более

 

Проведем группировку предприятий по признаку «Среднесписочная численность работников»

Группировка предприятий отрасли по среднесписочной численности работников

№ п/п	Интервал, чел.	Количество предприятий, попадающих в интервал	Накопленная частота
	меньше 130
	130 – 210
	210 – 290
	290 – 370
	свыше 370

 

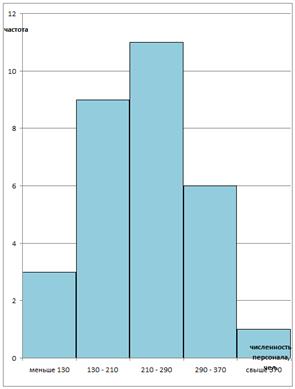
Рис. 2. Гистограмма численности персонала на предприятиях отрасли

 

Расчет средней арифметической, среднего квадратического отклонения, дисперсии

№ п/п	Интервал	Количество предприятий, попадающих в интервал (f)	Середина интервала (x')	xf	(x - )	(x- ) 2	f(x - )2
	меньше 130				-141	19975,11	59 925,33
	130 - 210				-61	3761,78	33 856,00
	210 - 290					348,44	3 832,89
	290 - 370					9735,11	58 410,67
	свыше 370					31921,78	31 921,78
Сумма					65742,22	187 946,67
Среднее (xcr)						6 264,89

 

Рассчитаем основные характеристики ряда распределения.

- средняя арифметическая взвешенная рассчитывается по формуле:

 

 

- среднее квадратическое отклонение (σ) рассчитывается по формуле:

 

 

- дисперсия (σ²) рассчитывается по формуле:

 

- коэффициент вариации рассчитывается по формуле:

 

 

Выводы:

Была произведена группировка предприятий отрасли по признаку «Среднесписочная численность работников».

Анализ сгруппированного ряда показал, что средняя численность рабочих на предприятиях отрасли составляет 231 человек. Амплитуда колебаний признака составляет 400 чел. Индивидуальные значения численности отклоняются от их средней величины на 79 чел. Средний квадрат отклонений индивидуального значения признака от среднего значения составляет 6264,89.

Значение коэффициента вариации признака равно 34 %, то есть находится в интервале от 0 до 40 % и можно говорить о том, что колеблемость признака незначительна. Однако значение коэффициента вариации больше 33 %, то есть распределение предприятий по данному признаку неоднородно и отличается от нормального.