Задача 2. Для исследуемого количественного признака Х генеральной совокупности получен интервальный статистический ряд
Для исследуемого количественного признака Х генеральной совокупности получен интервальный статистический ряд, представленный в таблице. В первой строке указаны интервалы значений 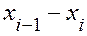 , а во второй – соответствующие частоты , а во второй – соответствующие частоты  (число значений признака Х, принадлежащих указанному интервалу). Требуется: (число значений признака Х, принадлежащих указанному интервалу). Требуется:
1. Построить полигон относительных накопленных частот (кумулятивную кривую).
2. Построить гистограмму частот и гистограмму относительных частот.
3. Найти моду, медиану, выборочную среднюю, выборочную дисперсию.
4. Проверить на уровне значимости  гипотезу о нормальном распределении признака Х генеральной совокупности по критерию согласия Пирсона. гипотезу о нормальном распределении признака Х генеральной совокупности по критерию согласия Пирсона.
5. В случае согласованности с нормальным распределением найти с надежностью  доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака Х генеральной совокупности. доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака Х генеральной совокупности.
2.1.

| 6,5-7,0
| 7,0-7,5
| 7,5-8,0
| 8,0-8,5
| 8,5-9,0
| 9,0-9,5
| 9,5-10
| 
|
|
|
|
|
|
|
|
2.2.

| 0,3-0,4
| 0,4-0,5
| 0,5-0,6
| 0,6-0,7
| 0,7-0,8
| 0,8-0,9
| 0,9-1,0
| 
|
|
|
|
|
|
|
|
2.3.

| 3-4
| 4-5
| 5-6
| 6-7
| 7-8
| 8-9
| 9-10
| 
|
|
|
|
|
|
|
|
2.4.

| 0,6-0,95
| 0,95-1,30
| 1,30-1,65
| 1,65-2,00
| 2,00-2,35
| 2,35-2,70
| 2,70-3,05
| 
|
|
|
|
|
|
|
|
2.5.

| 0,6-0,9
| 0,9-1,2
| 1,2-1,5
| 1,5-1,8
| 1,8-2,1
| 2,1-2,4
| 2,4-2,7
| 
|
|
|
|
|
|
|
|
2.6.

| 6,5-7,0
| 7,0-7,5
| 7,5-8,0
| 8,0-8,5
| 8,5-9,0
| 9,0-9,5
| 9,5-10
| 
|
|
|
|
|
|
|
|
2.7.

| 0,3-0,4
| 0,4-0,5
| 0,5-0,6
| 0,6-0,7
| 0,7-0,8
| 0,8-0,9
| 0,9-1
| 
|
|
|
|
|
|
|
|
2.8.

| 3-4
| 4-5
| 5-6
| 6-7
| 7-8
| 8-9
| 9-10
| 
|
|
|
|
|
|
|
|
2.9.

| 0,6-0,95
| 0,95-1,30
| 1,30-1,65
| 1,65-2,00
| 2,00-2,35
| 2,35-2,70
| 2,70-3,05
| 
|
|
|
|
|
|
|
|
2.10.

| 0,6-0,9
| 0,9-1,2
| 1,2-1,5
| 1,5-1,8
| 1,8-2,1
| 2,1-2,4
| 2,4-2,7
| 
|
|
|
|
|
|
|
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
Примеры решения типовых задач. Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2
Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2. Найдите константу диссоциации кислоты и значение рК.
Решение. Подставим данные задачи в уравнение закона разбавления
К = a2См/(1 –a) =...
|
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
Кишечный шов (Ламбера, Альберта, Шмидена, Матешука) Кишечный шов– это способ соединения кишечной стенки.
В основе кишечного шва лежит принцип футлярного строения кишечной стенки...
|
|

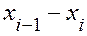 , а во второй – соответствующие частоты
, а во второй – соответствующие частоты  (число значений признака Х, принадлежащих указанному интервалу). Требуется:
(число значений признака Х, принадлежащих указанному интервалу). Требуется: гипотезу о нормальном распределении признака Х генеральной совокупности по критерию согласия Пирсона.
гипотезу о нормальном распределении признака Х генеральной совокупности по критерию согласия Пирсона. доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака Х генеральной совокупности.
доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака Х генеральной совокупности.



