Сущность деятельностного подхода в обучении математике
Исследование предмета математической деятельности и применение положения об единстве внешней (материальной) и внутренней (психической) деятельности позволило выявить деятельностное содержание в методике введения понятия, обучении доказательству теорем и решению задач, ориентированное на формирование у учащихся «знаний о знаниях» [127], «познавательного инструментария» [98, с. 90]. Деятельностный подход в обучении математике в средней школе можно успешно реализовать через формирование основных видов математической деятельности школьников на уроках. Для этого важно описание структуры каждого из них и, далее, процессов формирования этих видов деятельности у учащихся общеобразовательных учреждений, используя начатое в начальной школе развитие «общих учебных действий» [31, 128 и др.]. Основные виды математической деятельности учащихся отражены в методике обучения математике как познавательные процессы, подлежащие управлению со стороны учителя [24, 25, 40, 68, 75, 76 и др.]. Их выделение основано на содержании математического образования, представленного системой понятий и их признаков, оформленных в определениях (описаниях) и суждениях (аксиомах и теоремах), теоретические знания усваиваются в процессе решения разнообразных по значению и функциям задач. Поэтому в изучении математики в школе имеют место такие виды деятельности учащихся, как: введение понятия; изучение утверждений (обнаружение, формулировка аксиомы или теоремы, доказательство теорем); процесс решения задач. Выделенные виды математической деятельности учащихся представляются традиционными. Однако это не так. Иначе зачем нужна была бы постановка современной задачи школы — формирование математической компетентности учащихся. Для решения новой актуальной задачи в дидактике обозначены современные подходы к обучению: личностно ориентированный, деятельностный и др. [43]. Деятельностный подход в обучении ориентирует учителя на раскрытие детям личностного смысла учения, на развитие адекватного отношения школьников к учению. Поэтому мотивация учащихся на уроке математики, целеполагание в начале урока и на отдельных его этапах, реализующих тот или иной вид деятельности, является главным показателем деятельностной технологии обучения. Осуществление деятельностного подхода к введению понятия позволяет учащимся усваивать определение понятия не в его итоговойформе, основанной на запоминании формулировки, а получить в ситуации особо организованной аналитико-синтетической деятельности. Совокупность действий, составляющих деятельность «введение понятия», способствует раскрытию основного содержания, заключенного в понятии. Такой прием конкретно-индуктивного метода [40, 75, 100 и др.] введения математических понятий, как «прием отбора» [100, с. 15], или «конструктивный» [Там же, с. 16], выступает операцией действия определения понятия [68], позволяет ввести термин, обозначающий новый изучаемый объект. Операция формулировки определения в текстовой форме — итог активной самостоятельной работы каждого учащегося, результат действия определения понятия. Представление определения в символической записи — материализованная форма текстовой формулировки определения, обладающая ярко выраженной структурой, и потому наглядна. Словесная формулировка определения нового понятия для ученика представляет ни что иное, как перевод записанной формулы–определения с математического языка на естественный русский язык. Примеры определений понятий, приведенные выше (см. с. 41), хорошо иллюстрируют этот факт. Благодаря наглядности математической записи определения понятия выполнение действий выведение следствий определения и подведение под понятие доступны каждому учащемуся, так как овладение символикой является одним из аспектов формирования процессуальной стороны предмета математической деятельности. Например, следствием определения логарифма числа (логарифмом числа b по основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b [2, с. 224]) является утверждение Реализация деятельности «введение понятия» включает в себя выявление учащимися видов объектов, объединяемых определением понятия. Осуществляется выделение видов изученного понятия действием классификации понятия, являющегося родовым в данной теории, или обобщением понятия — для понятия, являющегося видовым. Деятельностный подход к изучению теоремы, решению задач, очевидно, заложен в современной методике изучения теорем, обучению решению задач [20, 75, 113 и др.]. Однако наблюдение опыта обучения математике в средней школе, результаты аттестации выпускников как девятых, так и одиннадцатых классов свидетельствуют о недостаточной деятельностной составляющей в их подготовке. Обучение доказательству математических утверждений невозможно без получения учащимися знаний о видах математических предложений, об их логической структуре. Как известно, к математическим предложениям относятся определения понятий, аксиомы, теоремы. Уже при изучении первых теорем необходимо, чтобы школьники представляли себе структуру математического утверждения и структуру его доказательства. Проблема овладения современными школьниками математическими понятиями, их определениями, свойствами понятий на продуктивном уровне отражается в статистике результатов ЕГЭ, аттестационных экзаменов за основную школу. Итоговая аттестация выпускников девятых классов по алгебре за 2008 год показывает, что на "5" с заданиями справились лишь 7,7% всех учащихся; на "4" – 19,9%; на "3" – 43,2%; на "2" – 29,2%. Т.е. почти треть выпускников девятилетней школы не усвоили базовый курс даже на оценку "3". Аналогичная ситуация и в 11 классах. За 2008 год пятерки получили лишь 9% всех выпускников, в то время как 23,5% имеют неудовлетворительную оценку. Таким образом, опыт современного образования, качество обучения математике всех выпускников ориентирует на дальнейшие исследования в области методики преподавания предмета, усиления путей адаптации психолого-педагогических исследований в сфере обучения математике школьников.
|

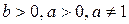 , вытекающее из определения и свойства знакопостоянства показательной функции. Символическая запись определения логарифма числа выглядит следующим образом: log
, вытекающее из определения и свойства знакопостоянства показательной функции. Символическая запись определения логарифма числа выглядит следующим образом: log  . Заметим, что выделенное следствие определения некоторые авторы включают в формулировку определения: log
. Заметим, что выделенное следствие определения некоторые авторы включают в формулировку определения: log  [82, с. 288]. Другим следствием определения логарифма числа является утверждение, известное как основное логарифмическое тождество:
[82, с. 288]. Другим следствием определения логарифма числа является утверждение, известное как основное логарифмическое тождество:  , получаемое заменой показателя х в равенстве
, получаемое заменой показателя х в равенстве 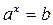 , входящем в определение, на log а b.
, входящем в определение, на log а b.


