Структура процесса решения задачПроцесс решения задачи (ПРЗ) мы рассматриваем как третий вид деятельности учащихся при обучении математике. В этом случае деятельность осуществляется для усвоения новых математических фактов (понятия или его свойства, алгоритма, метода). Причем данная потребность учащимися часто не осознается, но математические задачи как средство создания проблемной ситуации являются незаменимым способом мотивации школьников. Смыслообразующим мотивом процесса решения задачи, побуждающим фактором является нахождение решения задачи. Общая цель деятельности — нахождение ответа на главный вопрос задачи, задает следующие действия: 1) изучение структуры задачи; 2) поиск плана решения задачи; 3) осуществление плана решения (синтез); 4) проверка решения задачи; 5) изучение полученных результатов. Начиная с работы Д. Пойа [102], обозначившего структуру и содержание процесса решения задачи, исследование проблемы обучения решению задач продолжаются. Детализируются, углубляются, расширяются на основе имеющейся полувековой теории этого вопроса в методике преподавания математики списки приемов работы учителя и желаемых приемов работы учащихся [20, 40, 50, 52, 61, 72, 129 и др.]. Выводы о «необходимости воспитания у учащихся культуры решения задачи» [72, с.45] бесспорно верны. И в то же время они показывают, что на современном уровне развития методической науки и практики обучения математике эта проблема остается нерешенной. Причина видится в том, что идея воспитания познавательных привычек (формирования познавательного инструментария)при обучении решению задачи в традиционном обучении реализуется слабо. Как показывает в том числе данное исследование, она присуща деятельностному подходу к обучению. Чтение задачи, сопровождающееся построением ее наглядной модели (краткой записи, рисунка, чертежа), в которой выделены условие и требование (вопрос) задачи, означает наращивание операций, составляющих действие «изучение задачи» — первое действие ПРЗ (см. с. 45, 102–105). Обучение чтению математического текста, а задача является таким текстом [56, 96], следует начинать в том месте, где он появляется впервые, — в начальной школе. Также обстоит дело и с обучением поиску способа решения задачи — второго действия процесса решения задачи. Запаздывание на год–два ведет к дифференциации учащихся по уровню их математических способностей, которые зависят от свернутости процесса мышления [55]. И, как следствие, при организации работы над задачей на уроке возникают трудности руководства учителем функционирования деятельности учащихся всего класса. Дети, имеющие задатки, склонность к математике, исподволь, стихийно, действуя по образцу, который они улавливают в действиях учителя, научаются изучать структуру задачи. Другие — нет. Поэтому к 5–6 классу первые опережают одноклассников и на этапе изучения задачи, и на этапе поиска плана решения. Учитель математики в пропедевтическом курсе может ценой огромных усилий исправить эту ситуацию, используя имеющийся познавательный инструментарий (см. ниже, например, с. 103–106). Но, как показывают результаты современного контроля подготовки выпускников средней и особенно основной школы, деятельностью по решению задач (и математическими знаниями) многие из них не овладевают. Несмотря на имеющиеся многочисленные исследования по методике работы над задачей в обучении математике, представляется необходимым изложение этого вопроса с позиции деятельностного подхода к обучению — понимания деятельности как системы действий и составляющих их операций.
Действие 1. ИЗУЧЕНИЕ СТРУКТУРЫ ЗАДАЧИ Понимание задачи – первая цель деятельности учащихся при ее решении. Цель порождает соответствующее действие, которое осуществляется различными операциями. Результатом выполнения этого действия должно стать уяснение учеником фабулы задачи; осознание (познание) смысла отдельных слов и выражений, зависимости между данными задачи; видение связи данных с личным опытом, жизнью; осмысление условий, при которых возможна данная задачная ситуация; выделение главного вопроса задачи. Сущность действия заключается в том, что ученик, выполняя его, понимает текст задачи. Это выражается в умении выделять структуру задачи (условие, вопрос или требование); в видении зависимости между данными и искомыми величинами, в выделении главного вопроса задачи, в умении отразить структуру задачи, выбирая одну из моделей. Операции, составляющие действие изучение структуры задачи, следующие: а) чтение задачи; б) выделение условия и главного вопроса (требования) задачи; в) анализ текста задачи (внутренняя деятельность, результат ее материализованных действий — модель). Способ построения модели — результата анализа текста — зависит от сюжета (содержания) задачи. Представим примеры различных моделей задачи. Пример 1. Задача на движение Мотоциклист проехал до места назначения 330 км. В первые 3 ч он ехал со скоростью 60 км/ч, остальной путь он проехал за 2 ч. Во сколько раз скорость на втором этапе пути была больше, чем на первом? А. Табличный способ
Таблица 6
задавать при изучении текста задачи: – Какие объекты фигурируют в тексте задачи? – О каком процессе (явлении) идет речь в задаче? – Какие величины имеют место в этом процессе, каковы их значения? – Что известно о соотношении этих величин? Ию т.п. После решения задачи, в которой деятельность учащихся была явно управляема учителем (действие учеников «изучение структуры задачи» не функционировало), следует акцентировать внимание учащихся на вопросах, которые задавал учитель для достижения цели: понимания текста задачи. Усвоение, запоминание этих вопросов — ориентировочная основа действия «изучение структуры задачи». Приведенный небольшой перечень вопросов составляет тот познавательный инструментарий, который способствует формированию познавательной привычки — внимательному, осознанному чтению текста задачи. С другой стороны, привычка читать вдумчиво задачу представляет первую операцию рассмотренного действия. Следующая операция (и другая познавательная привычка) — моделирование задачной ситуации — наглядное изображение объектов (величин) и связей между ними в виде краткой записи задачи, схемы, рисунка. Результатом правильного понимания условия задачи является заполнение таблицы 6 (см. с. 102). Другие возможные примеры результата выполнения этой операции, приведены ниже: Б. Краткая схематическая запись
Время на I этапе – 3 часа Время на II этапе – 2 часа Весь путь – 330 км ? Во сколько раз больше скорость на II этапе, чем В. Схематический рисунок Последняя форма записи — схематический рисунок (рис. 26) — наиболее наглядна и потому представляется более целесообразной. Наглядность модели способствует целостному восприятию явления, осознанию взаимосвязей между данными условия и искомой величиной, ориентации на поиск способа решения задачи и даже, в данном конкретном случае, на способ нахождения искомого.
Рис. 26 Пример 2. Задача на дроби В магазин завезли фрукты и продали их за три дня. В первый день продали 30% всех фруктов, во второй день –
I день II день III день ? кг Рис. 27 Наглядная модель ориентирует на разные способы анализа и решения задачи. Приведем три из возможных моделей решения (два числовых выражения и уравнение). I) 168: (1 – II) 168: (1 – 0,3 – 0,7 · III) 0,3 х + 0,7 х · Пример 3. Задача на проценты Сочинение по русскому языку писали 90 выпускников школы. Им было предложено три темы: по Пушкину, по Маяковскому и свободная тема. Первую тему выбрали на 40% учеников больше, чем вторую, а третью – на 50% больше, чем первую. Сколько учеников писало сочинение по каждой теме? Результат первого действия для данной задачи наиболее наглядно представить с помощью линейной диаграммы (рис. 28).
   I? ч.
 II? ч. 90 уч.
Рис. 28
I
II 90 уч.
Рис. 29 Пример 4. Задача на движение в одном направлении Из одного города в другой выехали одновременно автобус со скоростью 53 км/ч и легковой автомобиль со скоростью 70 км/ч. Через 3 ч автомобиль прибыл в другой город. Сколько километров осталось ещё проехать автобусу? Более целесообразна модель задачи схемой-рисунком, иллюстрирующая характер движения: одновременного и в одном направлении (рис. 30). Приведенные четыре примера задач показывают явное преимущество представления результата первого действия — изучения текста задачи — схематическим рисунком. Можно говорить о воспитании познавательной привычки «рисовать задачу».
Действие 2. ПОИСК ПЛАНА РЕШЕНИЯ ЗАДАЧИ Как показывают методико-математические исследования и опыт обучения школьников решению задач, формирование действия поиска плана решения следует осуществлять на задачах с познавательной функцией [83] и так называемых ключевых (опорных) задачах [44, 130]. Приобретенный опыт и сформированное действие учащиеся применяют в тренировке при решении предлагаемых им задач на уроке и в форме домашнего задания. Выделяя главное в проблеме обучения школьников решению учебных математических задач с точки зрения деятельностного подхода, акцентируем внимание на вопросе формирования действия поиска как обобщенного приема, как эвристического средства решения задачи. Это второе ведущее действие, самое необходимое в познавательном инструментарии школьника и самое трудноформируемое на практике. Нахождение способа решения задачи — цель, задающая действие поиска плана решения. Наиболее продуктивным, как показывают теоретические исследования [52, 137 и др.], учебные пособия по методике обучения математике [20, 77, 113] и опыт обучения школьников поиску решения задачи [14, 129 и др.], является использование метода восходящего анализа. Подзадачи, появляющиеся в результате рассуждения по схеме восходящего анализа, представляют собой операционный состав действия. Приведем модели действия поиска плана решения — цепочки подзадач целенаправленного рассуждения для двух задач из рассмотренных выше четырех примеров. Построение модели поиска плана решения начинается, как известно, с требования задачи, которое выделено в ходе выполнения предыдущего действия. Для задачи, предложенной в первом примере (рис. 26, с. 103), модель поиска представлена на рисунке 31.
Рис. 31. Схема анализа к задаче примера 1 Ученик мысленно задаёт себе вопросы и отвечает на них, согласно схеме восходящего анализа: — Какой главный вопрос задачи? — Что достаточно знать, чтобы на него ответить? — Что из этого известно, а что нет? Какой новый вопрос возник? — Что достаточно знать, чтобы на него ответить? — Что из этого известно, а что нет? И т.д. В результате появляется план решения, последовательное нахождение: · длины первого этапа пути; · длины второго этапа пути; · скорости мотоциклиста на втором этапе пути; · сравнение скорости мотоциклиста на втором и на первом этапах пути. Для сравнения приведемпример модели действия поиска плана решения задачи менее сложной, по сравнению с первой, с одной стороны, но интересной тем, что она имеет различные способы решения.
Рис. 32. Схема I анализа к задаче примера 4 Решения задачи упрощается за счет использования понятия скорости сближения.
Рис. 33. Схема II анализа к задаче примера 4 В данном исследовании схемы анализа, приведенные выше, используются не только для анализа мыслительной деятельности субъекта [136], не только для формирования представления студентов и учителей о приемах организации поиска способа решения как соответствующего этапа работы над задачей [100]. В большей степени они играют роль средства для воспитания познавательной привычки — целенаправленного поиска при возникновении проблемной ситуации. Приведенные схемы анализа — модели поиска решения конкретной задачи, а, как известно, действие моделирования относится к общим учебным действиям, присущим учебной деятельности [33], и должно быть сформировано у учащихся уже в начальной школе. Научить ученика задавать себе такие вопросы, которые приводят к данным в условии задачи величинам и их значениям, — в этом суть формирования действия поиска плана при решении задачи. Ради этого выделяется процесс решения задачи как вид деятельности, в котором формируется действие поиска. Его значение важно и потому, что оно идентично по структуре с действием поиска плана доказательства утверждения, а деятельность ПРЗ по структуре близка ДИУ. Однако наблюдения и личный опыт работы в 5–6 классах показывают, что это действие — проведение рассуждения методом восходящего анализа — не бывает сформировано у каждого ученика. Оно проявляется в свернутом, неосознанном виде у наиболее подготовленных школьников. Возникает противоречие: оказывается, что в начале обучения математике в средней школе (в пятом классе) учащиеся не владеют действием, без которого процесс решения задачи как деятельность функционировать не может. Но и сегодня считается, что организуемая работа по решению задачи — деятельность. Чья? Совместная деятельность учителя и учащихся? И снова вопрос: не запаздываем ли мы с передачей выполнения этой деятельности «самому ученику для самостоятельного осуществления без вмешательства учителя» [150, с. 53]? Для формирования у школьников действия анализа (поиска плана решения задачи ) однажды каждый ученик должен осознать, что следует знать общий приём рассуждений, который приведёт его к плану решения задачи. В такой момент появляется мотив деятельности, направленной на овладение методом восходящего анализа. Именно в этой ситуации «срабатывают» сформированные в учебной деятельности школьников действия «преобразования ситуации для обнаружения всеобщего отношения рассматриваемой системы» и «моделирование выделенного отношения в предметной, графической и знаковой форме» [33, с.15]. Осуществить мотивацию для изучения сущности поиска плана решения задачи (развернуть действие в деятельность — по А.Н. Леонтьеву) можно на задаче, решение которой вызывает у учащихся познавательное затруднение — проблемную ситуацию. Примером такой задачи является, например, для пятиклассников и задача, модель поиска которой представлена на рис. 26, и следующая достаточно сложная задача. Лодка, скорость которой в стоячей воде 12 Модель поиска (рис. 34) может быть построена учащимися пятого класса в
Рис. 34 групповой работе или в совместной работе с учителем. Выполнение действий контроля и оценки, предполагающее «обращение внимания школьника к содержанию своих собственных действий, к рассмотрению их особенностей с точки зрения требуемого задачей результата» [33, с. 19], называемое рефлексией, является существенным условием формирования деятельности (действий) учащихся. Неоднократное и целенаправленное использование модели поиска в проблемных ситуациях (а таковые возникают часто как на уроке, так и при выполнении домашней работы) позволяет учащимся выделить и осознать операционный состав действия по отысканию пути решения задачи (метод восходящего анализа), положительно оценить и принять его. К сожалению, результаты итоговых испытаний последних лет показывают, что такими действиями, как изучение условия задачи и поиск плана ее решения учащиеся овладевают слабо, а это значит, что самостоятельно решить сколько-нибудь новую задачу они не могут. Поэтому формирование этих действий должно быть целенаправленным, планомерным и систематическим в начальной школе. В пятом и шестом классах «процесс постепенной передачи выполнения отдельных элементов этой деятельности самому ученику» [150, с. 53] должен быть завершен. Действие 3.ОСУЩЕСТВЛЕНИЕ ПЛАНА РЕШЕНИЯ Третье действие — осуществление плана решения задачи, как правило, не вызывает у учащихся особых затруднений, если найден план решения задачи (выполнено второе действие ПРЗ). Необходимо провести лишь пошаговое выполнение всех пунктов плана решения. В мыслительном плане школьники осуществляют синтез. Модель решения задачи может быть следующей: ( У1&У2 На рисунках 35 и 36, а также в приведенных ниже решениях (с. 104–105) представлены модели синтеза — различные способы осуществления решения задачи четвертого примера (см. ниже, с. 113).
Рис. 35. Схема синтеза к задаче примера 4 (решение 1)
Рис. 36. Схема синтеза к задаче примера 4 (решение 2) Решение в вопросно-ответной форме (вторая модель синтеза) 1. Какова длина пути автобуса за 3 часа?
2. Какова длина всего пути?
3. Сколько километров осталось ещё проехать автобусу? 210 – 159 = 51 (км) Ответ: автобусу осталось проехать 51 километр. Решение с пояснением (третья модель синтеза) 1. 2. 3. 210 – 159 = 51 (км) – осталось ещё проехать автобусу. Ответ: автобусу осталось проехать 51 километр. Составление числового выражения (четвертая модель синтеза) Длина пути автобуса за 3 часа: Расстояние между городами Автобусу осталось проехать: ( Находят значение числового выражения: Ответ: автобусу осталось проехать 51 километр. Решение в виде действий (пятая модель синтеза) 1. 2. 3. 210 – 159 = 51 (км) – осталось ещё проехать автобусу. Ответ: автобусу осталось проехать 51 километр. Действие 4.ПРОВЕРКА РЕШЕНИЯ ЗАДАЧИ Общее учебное действие контроля выполнения предыдущих действий (см. с. 5) в деятельности ПРЗ имеет целью выяснить, согласуется ли найденный результат (числовое значение выражения, корня уравнения или устанавливаемый факт, построенный объект) с условием и требованием задачи, выясняется, правильно ли понята задача. Операции, составляющие это действие, общеизвестны. Во-первых, это проверка результата по смыслу задачи. Довольно часто возникают ситуации, когда модель дает вариант ответа, который не подходит по смыслу к условию задачи. Например, скорость, время, расстояние, производительность, работа и другие физические величины не выражаются отрицательным числом; при подсчете предметов или людей получаются натуральные числа и т.п. Вторая операция — проверка правильности решения задачи. Способ проверки зависит от конкретной задачи. В задаче примера 4 проверку можно осуществить путем составления и решения одной из обратных задач. Например: Из одного города в другой выехали одновременно автобус со скоростью 53 км/ч и легковой автомобиль. Через 3 ч автомобиль прибыл в другой город, а автобусу осталось ещё проехать 51 км. Какова была скорость легкового автомобиля? На рис. 37 представлена наглядная модель этой задачи, ниже — ее решение. Рис. 37 Решение: ( Действие 5.ИЗУЧЕНИЕ РЕШЕНИЯ ЗАДАЧИ Целью данного действияПРЗ является рефлексия действий, выполненных учащимися. Оценка способа решения данной задачи — конкретизация общего учебного действия [33]. Структуру данного действия ПРЗ составляют операции: осмысление ответа и его полная запись и решение задачи другим способом (см., например, с. 111). Эти операции являются средством воспитания познавательной привычкизавершать работу над задачей, осуществляя «взгляд назад» [102].
|
При обучении табличная модель, как и любая другая (см. ниже), составляется по ходу диалога учителя и учащихся по тексту задачи. При этом учитель на нескольких первых уроках демонстрирует вопросы, которые следует
Скорость на I этапе – 60 км/ч
остатка, а в третий день – остальные 168 кг. Сколько всего килограммов фруктов завезли в магазин?
остаток
30 % 
III? ч.
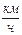, шла по течению реки 3 часа. Найти время, затраченное лодкой на путь, пройденный против течения, если его длина на 8 км больше пути, пройденного по течению реки, а скорость течения реки 4 
.
Путь, пройденный лодкой по течению
Скорость лодки по течению
? 
Скорость лодки в стоячей воде
П1 ) & … ( Уi&Пк 
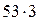(км)
(км)
(км).
(км).
