Д. Пойа
4.3.1. Структура деятельности «изучение утверждений» Деятельность по изучению понятия на уроке математики переходит в изучение его свойств, представленных чаще всего в виде теоремы. Деятельность по изучению утверждений (ДИУ) и процесс решения задачи имеют много общего по структуре, поскольку представляют собой различные способы применения знаний о понятиях и их свойствах. Можно сказать, эти виды деятельности порождаются первой — деятельностью введения новых понятий. Выделение видов деятельности необходимо для их изучения и осуществления деятельностного подхода в математике. В учебном процессе одна деятельность сменяется другой или входит в другую. Так, при изучении арифметического квадратного корня из числа а действия, составляющие деятельность по изучению понятия, сменяются действиями следующего вида деятельности. Деятельность по изучению утверждений (теорем) осуществляется следующими действиями: · обнаружение свойства, его формулировка (выдвижение гипотезы); · изучение структуры математического предложения; · поиск плана доказательства; · доказательство утверждения; · изучение результатов деятельности: выведение следствий теоремы, ее обобщение, различные способы доказательств. Последнее действие представляет собой конкретизацию общих учебных действий контроля и оценки [33, с. 15] для особого предмета деятельности — теоремы и ее доказательства. Как показывает опыт, дети очень любят «открывать» новые знания, устанавливать закономерности. Использование деятельностного подхода в обучении именно на этом и основывается. Для понятия арифметического квадратного корня ситуация, приводящая к открытию свойства, легко создается заданиями на вычисление значений выражений, например, следующих: Формулировкой гипотезы (теоремы) завершается первое действие деятельности по изучению утверждений. 3а ним следует действие, направленное на изучение структуры теоремы. Суть этого действия заключается в преобразовании словесной формулировки: запись на математическом языке, выделение (если возможно) условия и заключения теоремы, уточнение значения параметров. В рассматриваемом примере изучения свойства арифметического квадратного корня в восьмом классе [4] его полная запись может быть следующей: Итак, нужно доказать истинность равенства – Что достаточно, чтобы утверждать истинность этого равенства? Ответ на вопрос будет сформулирован, благодаря выполнению действия «подведение под понятие» арифметического квадратного корня. – Достаточно показать, что выражение 1) существование выражения 2) Составленный план доказательства показывает, что цель, породившая действие, достигнута, ход доказательства найден, и учащиеся переходят к выполнению следующего действия — осуществления доказательства. Таблица 4
В таблице 4 представлено полное, подробное рассуждение (цепочка силлогизмов), являющееся доказательством этого свойства. Ученик должен понимать суть приведенного доказательства, осознавать каждый этап этого рассуждения. Во внешних действиях этот процесс проявляется в «свернутом» виде. Еще более свернуто доказательство теоремы, представленное в учебнике [4, 80]. К моменту изучения свойств арифметического квадратного корня учащиеся должны уже овладеть деятельностью по доказательству теоремы. Формирование ее, убеждение в необходимости доказательств и обучение действиям, составляющим этот вид математической деятельности учащихся, в настоящее время приходится на 5-6 классы по некоторым программам обучения [37, 38]. Однако в большинстве своем формирование указанного вида деятельности при обучении математике осуществляется в начале изучения систематического курса алгебры и геометрии. Причем традиционный курс алгебры седьмого класса представлен в основном изучением целых выражений, тождественных преобразований одночленов и многочленов. Теоремы, в которых раскрываются свойства степени с натуральным показателем, формулы сокращенного умножения, по структуре заметно отличаются от теорем курса геометрии. Если первые геометрические теоремы импликативны, то теоремы традиционного курса алгебры имеют вид теорем – тождеств. Поэтому формирование знаний о теореме и ее структуре следует выполнять и при изучении теорем курса алгебры, и при изучении геометрии. Только в том случае, когда в курсе алгебры седьмого класса при изучении числовых выражений рассматриваются свойства числовых неравенств, имеющие импликативную структуру [104, с. 22], можно выделять условие и заключение теоремы, подчеркивая общность математических предложений — теорем. Как видно из примера (табл. 4), построение доказательства основано на умении учащихся выполнять «подведение под понятие» и «выведение следствий». Еще раз отметим важность организации полноценной деятельности по изучению понятия (в данном случае — понятия «доказательства»), и в самом начале обучения школьников доказательству утверждения – иллюстрации сути доказательства. Примеры дедуктивных рассуждений при изучении первых теорем курса геометрии приведены выше (см. с. 14, 74). Опыт показывает, что «свернуть» полное дедуктивное рассуждение уместно после изучения первого признака равенства треугольников. Приведем еще раз пример модели дедуктивного рассуждения в обучении: доказательство первого признака равенства треугольников.
Положение о формировании познавательного инструментария учащихся (см. с. 33) требует, чтобы для осуществления действия поиска доказательства ученик знал его смысл[17] и операциональный состав (см. выше с. 89 и ниже с. 95). Аналогично для формирования действия осуществления доказательства учащиеся должны знать, что такое доказательство и как его построить. «Открытие» доказательства учащимися требует знания ими процедуры дедуктивного выведения из условия теоремы ее заключения, а для доказательства формулы — выведения истинности утверждения, заключенного в ней (см. с. 64). Если предыдущее действие реализовано в полном объеме, т.е. посредством рассуждения методом восходящего анализа поиск достаточных условий доведен до условия теоремы, то теорема, доказана[18] (или задача решена). В случае, когда найдена идея доказательства, данное действие выполняется синтетическим методом. Однако формирование действия доказательства утверждения, одного из составляющих познавательного инструментария, которым должен овладеть каждый ученик, следует начинать (и при необходимости постоянно к нему обращаться) с дедуктивного вывода. 4.3.2. Структура действий деятельности «изучение утверждений» Изучение утверждения как деятельность состоится в результате выполнения пяти действий (см. с. 89), каждое из которых соответствует частной цели, определенной мотивом ДИУ: 1) «открыть» новое свойство изучаемого понятия; 2) сформулировать открытое свойство как математическое предложение; 3) «открыть» доказательство истинности сформулированной теоремы; 4) выполнить доказательство; 5) исследовать результат деятельности. Первая цель задает действие «обнаружение свойства, его формулировка». Его структуру составляют операции: · выдвижение гипотезы (индивидуально или в групповой работе на основе выполнения упражнений, подводящих к «открытию» нового свойства изучаемого объекта); · обобщение результатов индуктивного поиска нового свойства; · формулировка теоремы. Вторая цель задает действие «изучение структуры математического предложения». Это действие реализуется следующей совокупностью операций: · формулировка предложения в логической форме (выделение условия и заключения для импликативной теоремы); · установление вида теоремы; · символическая запись теоремы (конкретизация формулировки в принятых символических обозначениях, в том числе выполнение чертежа). Третья цель задает действие «поиск плана доказательства». Целенаправленным поиском доказательства теоремы является, как известно, восходящий анализ. Схема восходящего анализа: An Четвертая цель задает действие «доказательство утверждения». Построение силлогизмов — операции, составляющие действие «доказательство утверждения». Как видно из примера, эти операции представляют собой «подведение под понятие» и «выведение следствий». Их упорядоченный синтез – доказательство. Этот момент убедительно показывает взаимосвязь и взаимообусловленность двух видов математической деятельности учащихся. Действия ДВП способствуют формированию действия «доказательство утверждения», а формирование этого действия ДИУ неявно (а можно при необходимости его использовать явно) служит мотивацией ДВП, изучаемых в дальнейшем. Как следует из вышесказанного (с. 64 – 67, 89 – 94), операциями, составляющими это действие, являются дедуктивные выводы — построение цепочек силлогизмов в их полном или кратком виде. Как отмечено выше, эти операции осуществляются на основе правил логического вывода. Их синтез представляет доказательство утверждения. Наконец, пятая цель задает действие «изучение результатов деятельности». Это действие выполняется на основе сформированных у учащихся общих действий контроля и оценки и реализуется следующей совокупностью операций: · выведение частных следствий; · выведение следствий теоремы или ее обобщение; · поиск различных способов доказательства теоремы. «Выведение частных следствий» в практике обучения принято называть первичным закреплением. Это решение задач с дидактической функцией. В условиях таких задач обычно задается ситуация, аналогичная теореме. Использование изученной теоремы в качестве обоснования позволяет получить требуемое заключение (тезис). Например, для изучения результатов деятельности по изучению свойства арифметического квадратного корня (см. с. 89) фигурируют различные вариации значений переменных а и b и выражений Выведение следствий теоремы и ее обобщение основано на рассмотрении частных случаев, т.е. связано с научными методами индукции, классификации, конкретизации. Различные способы доказательства теоремы получаются при подборе разных достаточных условий в структуре метода восходящего анализа, если осуществляется оценка найденного способа доказательства. Выделение структуры деятельности по изучению утверждений, операционального состава действий, посредством которых она осуществляется, выпукло показывает тот познавательный инструментарий, которым должны овладеть учащиеся. Это «знания о знаниях». Во-первых, ДИУ будет сформирована у школьников только в том случае, если они овладеют знаниями: · о теореме как утверждении, истинность которого доказана; · о видах теорем, полученных классификацией по их логической структуре; · о доказательстве как цепочке истинных умозаключений, идущих от исходных посылок к доказываемому тезису. Во-вторых, формирование ДИУ зависит от знаний учащихся о методах анализа (восходящего и нисходящего) и синтеза, а также об индуктивных и дедуктивных умозаключениях и от умения их применять (сформированность соответствующих компетенций). Наконец, овладение отмеченными знаниями и методами невозможно без использования математического языка: символов, обозначающих понятия, отношения и операции.
|

 и
и 
 ;
;  и
и 
 ;
; 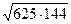 и
и 
 . Наблюдение и сравнение результатов вычислений приводят учащихся к обобщению, на основе которого выдвигается гипотеза — словесная формулировка утверждения.
. Наблюдение и сравнение результатов вычислений приводят учащихся к обобщению, на основе которого выдвигается гипотеза — словесная формулировка утверждения.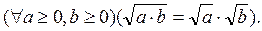 Структура этого свойства имеет вид
Структура этого свойства имеет вид 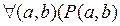 , по которому определяется вид теоремы: «теорема–тождество» [11, с. 49]. С появлением символической записи свойства можно считать действие по изучению теоремы реализованным, и далее «включается» следующее действие — поиск плана доказательства. Целенаправленный поиск доказательства утверждения — эвристическая, внутренняя деятельность ученика, внешнее проявление которой наблюдается умением ставить нужные вопросы и отвечать на них. Это общие вопросы, в методике преподавания математики они известны как составляющие рассуждения методом восходящего анализа [75].
, по которому определяется вид теоремы: «теорема–тождество» [11, с. 49]. С появлением символической записи свойства можно считать действие по изучению теоремы реализованным, и далее «включается» следующее действие — поиск плана доказательства. Целенаправленный поиск доказательства утверждения — эвристическая, внутренняя деятельность ученика, внешнее проявление которой наблюдается умением ставить нужные вопросы и отвечать на них. Это общие вопросы, в методике преподавания математики они известны как составляющие рассуждения методом восходящего анализа [75]. .
. является арифметическим квадратным корнем из выражения а·b, т.е. достаточно обосновать:
является арифметическим квадратным корнем из выражения а·b, т.е. достаточно обосновать: и его неотрицательность (
и его неотрицательность (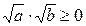 );
);


 существуют
существуют




 )2
)2
 )2 = (
)2 = ( )2·(
)2·( )2
)2
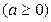 ,
(
,
( )2,
)2, 
 )2 = =(
)2 = =(
 ,
,

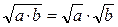
 АВС (*),
АВС (*),  А 1 В 1 С 1(**),
АВ = А 1 В 1 (***),
АС=А 1 С 1(****),
А 1 В 1 С 1(**),
АВ = А 1 В 1 (***),
АС=А 1 С 1(****),
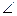 А =
А = 

 С1 С2 С1 С2
А1 В1 В2 А1 В1(В2)
Рис. 25 (а) Рис. 25 (б)
С1 С2 С1 С2
А1 В1 В2 А1 В1(В2)
Рис. 25 (а) Рис. 25 (б)
 An- 1
An- 1 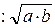 ,
, 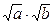 . Как правило, такие упражнения достаточно полно представлены в учебниках.
. Как правило, такие упражнения достаточно полно представлены в учебниках.


